归并排序详解-优快云博客

2019独角兽企业重金招聘Python工程师标准>>>

如果有1个数组，数组的左半部分和右半部分都已经排好序，如何将该数组合成1个有序的数组？

开辟1个同样大小的临时空间辅助我们完成归并过程，如下图

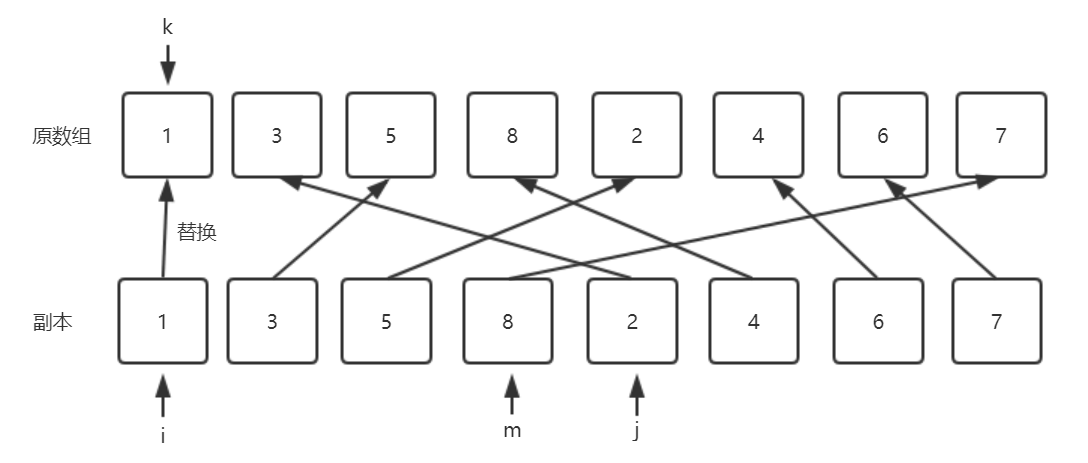
k:表示归并过程中，当前需要替换的原数组位置

i，j：要替换k位置的数据，当前需要考虑的元素，也就是从i和j位置中的元素中取1个最小的，替换到原数组k的位置。

m：中间位置，也就是数组左半部分最大的索引位置。

第一次：i和j位置的元素比较，1比2小，则将1替换k的位置，然后i++，k++；

第二次：i和j位置的元素比较，3比2大, 则将2替换k的位置，然后j++，k++；

依次类推,最后原数组就变成了1个有序的数组，这就是归并的过程。

代码实现：

    /**
     * 合并函数
     * @param arr   原始数组
     * @param left  要合并数组的最左侧索引位置
     * @param mid   左侧有序数组和右侧有序数组的分界线
     * @param right 要合并数组的最右侧索引位置
     */
    void __merge(int[] arr, int left, int mid, int right) {
        //将arr数组 left~right之间的元素copy到arrCopy中
        int[] arrCopy = new int[right - left + 1];
        for (int i = left; i <= right; i++)
            arrCopy[i - left] = arr[i];//赋值

        int i = left, j = mid + 1;
        //给arr数组left ~ right之间的数组赋值
        for (int k = left; k <= right; k++) {
            if (i > mid) {//如果i大于mid,说明左侧已没有可以赋值的元素，则选取右侧的元素
                arr[k] = arrCopy[j - left];
                j++;
            } else if (j > right) {//说明右侧已没有赋值的元素，则选取左侧的元素
                arr[k] = arrCopy[i - left];
                i++;
            } else if (arrCopy[i - left] < arrCopy[j - left]) {//左侧元素小于右侧元素，选取左侧元素
                arr[k] = arrCopy[i - left];
                i++;
            } else {//否则选取右侧元素
                arr[k] = arrCopy[j - left];
                j++;
            }
        }
    }

测试：

    @Test
    public void test__merge(){
        int[] arr = new int[]{1,3,5,8,2,4,6,7};
        int left = 0;
        int right = arr.length - 1;
        int mid = (left + right)/2;
        __merge(arr,left,mid,right);
        Arrays.stream(arr).forEach(item->{
            System.out.print(item + " ");
        });
    }

测试结果如下，从测试结果可以看出，数组已经变成一个有序的数组。

如果我们要对数组 5,1,3,8,7,4,6,2 进行排序，可以将其分为两个大小各为4的子数组，对两个子数组进行排序，然后合并它们，生成有序数组。同样，可以将每个子数组，再次划分成两个子数组，然后对子数组进行排序和合并。依次划分，直到子数组大小变为1。这样就可以将一个无序的数组变成有序的数组。

代码实现：

    /**
     *递归使用归并排序,对arr[left....right]范围进行排序
     * @param arr
     * @param left
     * @param right
     */
    public void mergeSort(int[] arr,int left,int right){
        if (left >= right)//如果只有1个元素，返回
            return;
        int mid = (left + right)/2;
        mergeSort(arr,left,mid);//整个函数执行完,arr[left....mid]变成有序
        mergeSort(arr,mid + 1,right);//arr[mid + 1....right]变成有序
        __merge(arr,left,mid,right);//合并后，arr[left....right] 变成有序。
    }

测试

    @Test
    public void test__mergeSort(){
        int[] arr = new int[]{5,1,3,8,7,4,6,2};
        int left = 0;
        int right = arr.length-1;
        mergeSort(arr,left,right);
        Arrays.stream(arr).forEach(item->{
            System.out.print(item + " ");
        });
    }

从运行结果可以看出数组已经排好序。

时间复杂度分析

我们假设对n个元素进行归并排序需要的时间为T(n),那么分解成两个子数组排序的时间都是T(n/2),__merge合并两个子数组的时间复杂度为O(n)，则归并排序的时间复杂度公式如下：

T(1) = C；   n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = 2*T(n/2) + n； n>1

通过这个公式，进行分解：

T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
     = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
     ......
     = 2^k * T(n/2^k) + k * n
     ......

当 T(n/2^k)=T(1) 时，也就是 n/2^k=1，可以得到k=log2n，所以T(n) = nlog2n+Cn。用大O表示法的话，其时间复杂度为O(nlogn).

归并排序的执行效率与原始数组的有序程度无关，所以是非常稳定的排序算法，最好、最坏、平均时间复杂度都是O(nlogn)。

优化一：

由于归并排序mid两侧的元素都是有序的，如果arr[mid]<=arr[mid + 1] 就没有必要再做归并排序了

    public void mergeSort2(int[] arr,int left,int right){
        if (left >= right)//如果只有1个元素，返回
            return;
        int mid = (left + right)/2;
        mergeSort(arr,left,mid);//整个函数执行完,arr[left....mid]变成有序
        mergeSort(arr,mid + 1,right);//arr[mid + 1....right]变成有序
        //由于归并排序mid两侧的元素都是有序的，如果arr[mid]<=arr[mid + 1] 就没有必要再做归并排序了
        if(arr[mid] > arr[mid + 1])
        __merge(arr,left,mid,right);//合并后，arr[left....right] 变成有序。
    }

优化2：

当元素数量比较少时，使用插入排序要比归并排序效率要好。

    public void mergeSort3(int[] arr,int left,int right){
        if (right - left <= 30 )//如果只有30个元素，插入排序
            insertionSort(arr,left,right);
        int mid = (left + right)/2;
        mergeSort(arr,left,mid);//整个函数执行完,arr[left....mid]变成有序
        mergeSort(arr,mid + 1,right);//arr[mid + 1....right]变成有序
        //由于归并排序mid两侧的元素都是有序的，如果arr[mid]<=arr[mid + 1] 就没有必要再做归并排序了
        if(arr[mid] > arr[mid + 1])
            __merge(arr,left,mid,right);//合并后，arr[left....right] 变成有序。
    }


    /**
     * 对arr[l...r]范围的数组进行插入排序
     * 将未排好序的部分最左侧的数据拿出和已排好序的数据进行比较，然后找到合适的位置插入。
     * 重复这个过程，直到未排序部分的数据为空为止。
     * @param arr
     * @param left
     * @param right
     */
    void insertionSort(int arr[], int left, int right){
        for( int i = left + 1 ; i <= right ; i ++ ) {
            int e = arr[i];//arr[i]未排好序最左侧的数据
            int j;//j为要插入的位置，初始位i这个位置，也就是未排好序最左侧的索引位置
            //寻找要插入的位置，如果j == left，说明已经到了最左侧的数据，left的位置就位要插入的位置
            //当j > left && arr[j-1] > e时，则将arr[j-1]的元素放到j这个位置上，同时j--
            //直到循环跳出，j的位置就是要插入的位置。
            for (j = i; j > left && arr[j-1] > e; j--)
                arr[j] = arr[j-1];//arr[j-1]向右移1位,就空出了
            arr[j] = e;
        }
        return;
    }

转载于:https://my.oschina.net/suzheworld/blog/3040576