用几何画板绘制数学图形有哪些技巧

作为数学老师，你是不是整天都在为准确备课笔记而发愁，一想到有很多几何图就觉得头疼，不知不觉中就得了备课恐惧症。不用怕！用几何画板来帮助你画几何图，绝对会让你的备课恐惧症瞬间消失！

几何画板免费获取地址：http://www.mairuan.com/product/jihehuaban

使用几何画板备课的好处就是可以动态演示图形变化过程，可以实现在黑板上无法实现的效果，黑板上是无法让图形动起来的，图形无法实现旋转、折叠等效果，可是几何画板就不一样了，它被称为“21世纪动态几何”，可以让图形动起来，并且还保持几何关系不变，老师们都在用它来讲课。要想学好几何画板，下面的几个画图技巧，你一定要掌握，做课件的时候绝对用的上！

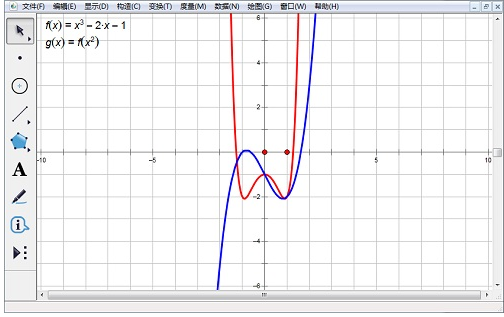
一、用几何画板画复合函数图像

比如，已知函数f（x）=x3-2x-1，绘制f（x）和f（x2）两个函数的图象，具体步骤如下：

1.选择“数据”--“新建函数”，“方程”选择“y=f（x）”，在函数对话框中输入“x”、“^”、“3”、“-”、“2”、“x”、“-”、“1”，“确定”。

2.选择“数据”--“新建函数”，弹出编辑函数对话框，点击函数解析式“f（x）”，此时，编辑框中出现“f（）”格式，在括号内输入“x”、“^”、“2”，确定，绘图区域中会出现“g（x）=f（x2）”。

3.分别选中绘图区域中的函数解析式，右键选择“绘制函数”，系统自动绘制函数图象。

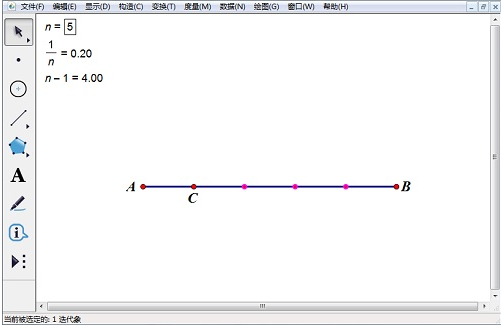
二、用几何画板n等分线段

借用几何画板强大的绘图功能你可以构造出任何你想要图形，不管是旋转组合还是将图形等分。都可以轻松实现，几何画板实现线段n等分的方法如下：

1.新建参数。选择“数据”--“新建参数”新建参数n，初值设为5，单位无，选中n后点击“数据”--“计算”，分别计算出1/n和n-1的值。

2.构造线段及线段上的点。利用线段工具绘制一条线段AB，选定线段AB和1/n，单击“绘图”--“在线段上绘制点”，得到点C。

3.构造等分点。隐藏线段AB，选定点A、参数n和数值n-1（作为迭代深度），按住Shift键，单击“变换”--“深度迭代”，在A的初象处点击C，n的初象处点击n-1。此时会出现迭代数据表，单击“结构”，选定“生成迭代数据表”，把前面的勾去掉，单击“迭代”。

4.在空白区域点击右键，选择“显示所有隐藏”显示线段AB，可以得到如下图的n等分线段效果。通过改变参数改变等分数。

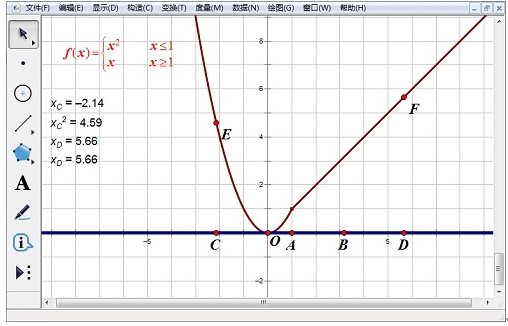
三、用几何画板画分段函数

函数图象有很多，在很多情况下，函数图象并不是由一个函数组成的，而是由几个组合而成，比如分段函数。那么几何画板怎么画分段函数呢？

具体操作如下：

1.选择“绘图”--“定义坐标系”原点标签为“O”，单位点标签为“A”。 依次选中点A和点O，选择“构造”--“射线”构造出射线AO，即为区间x≤1。 利用点工具在点A右边作出任意一点B，绘制出射线AB。

2.利用“点”工具， 在x轴上，点A的左边和右边分别绘制出点C和点D，选中点C，选择“度量”--“横坐标”度量出点C的横坐标。选择“数据”--“计算”，弹出“计算器”对话框，依次单击“xc”、“^”、“2”，“确定”。选中xc和计算值，选择“绘图”--“绘制点（x，y）”命令绘制出点“E”。

3.依次选择点C和点E，选择“构造”--“轨迹”菜单命令，绘制出区间函数图像。

4.同样的方法度量出点D的横坐标值，选择“数据”--“计算”菜单命令，在对话框中单击“xD”，“确定”。选中两个xD，选择“绘图”--“绘制点（x、y）”菜单命令，绘制出点F。

5.选中点D和点F，选择“构造”--“轨迹”菜单命令，绘制出区间内函数y=x的图像。在Word中编辑好分段函数的表达式复制粘贴到几何画板中。

上面三个在几何画板里面的画图技巧看似简单，其实包含的很多的技巧，也只有在熟练掌握该软件之后才能快速画出这些图形或图像。几何画板功能非常强大，画图时擅用其菜单功能，往往会事半功倍，非常轻松就能完成备课。以上画图技巧对你制作教学课件绝对有帮助，你在编辑数学试卷时也绝对能用得上！

转载于:https://www.cnblogs.com/MathType/p/5782984.html