栈与队列

最新推荐文章于 2025-08-15 23:10:13 发布

转载最新推荐文章于 2025-08-15 23:10:13 发布 · 71 阅读

文章标签：

数据结构，是数据的组织形式，包括存储方式和访问方式两层含义，二者是紧密联系的。例如，数组的各元素是一个挨一个存储的，并且每个成员的大小相同，因此数组可以通过下标访问的方式，结构体的各成员也是一个挨一个存储的，但是每个成员的大小不同，所以只能用.运算符加成员来访问，而不能按下标访问。

一个问题中的存储方式和访问方式（即数据结构）就决定了解决问题可以采用说明样的算法。要设计一个算法就要同时设计相应的数据结构来支持这种算法。

用数组实现堆栈（如果堆栈中存储类型相同）

用数组实现栈/*
 * use [] implement stack
 * author : kevin
 * date : 2012.09.30
 */

#include <stdio.h>

char stack[512];
int top;

void push(char c)
{
	stach[top++];
}	

char pop(void)
{
	return stack[--top];
}

int is_empty(void)
{
	return top == 0;
}

int main(void)
{
	push('a');
	push('b');
	push('c');

	while (!is_empty) 
		putchar(pop());
	putchar('\n');

	return 0;
}

栈的特点就是“后进先出”。

用递归实现倒叙打印

用递归实现栈/* 
 * digui implement unsort
 * author : kevin
 * date : 2012.09.30
 */

#include <stdio.h>
#define LEN 3

char buf[LEN] = {'a', 'b', 'c'};

void print_backward(int pos)
{
	if (pos == LEN)
		return ;
	print_backward(pos+1);
	putchar(buf[pos]);
}

int main(void)
{
	print_backward(0);
	putchar('\n');

	return 0;
}

回溯

迷宫问题，深度优先搜索

迷宫/* 
 * user shuzi implement migong
 * arthur : kevin
 * date : 2012.09.30
 */

#include <stdio.h>

#define MAX_ROW 5
#define MAX_COL 5

struct point {
	int row, col;
} stack[512];
int top = 0;

void push(struct point p)
{
	stack[top++] = p;
}

struct point pop(void)
{
	return stack[--top];
}

int is_empty(void)
{
	return top == 0;
}

/* 1 wall , 0 road */
int maze[MAX_ROW][MAX_COL] = {
	{ 0, 1, 0, 0, 0 },
	{ 0, 1, 0, 1, 0 },
	{ 0, 0, 0, 0, 0 },
	{ 0, 1, 1, 1, 0 },
	{ 0, 0, 0, 1, 0 }
};

void print_maze(void)
{
	int i, j;
	for (i=0; i<MAX_ROW; i++) {
		for (j=0; j<MAX_COL; j++)
			printf("%d ", maze[i][j]);
		putchar('\n');
	}
	printf("*********\n");
}

/* record for the before point */
struct point predecessor[MAX_ROW][MAX_COL] = {
	{ {-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1} },
	{ {-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1} },
	{ {-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1} },
	{ {-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1} },
	{ {-1,-1},{-1,-1},{-1,-1},{-1,-1},{-1,-1} }
};

void visit(int row, int col, struct point pre)
{
	struct point visit_point = { row, col };
	maze[row][col] = 2;
	predecessor[row][col] = pre;
	push(visit_point);
}

int main(void)
{
	struct point p = {0, 0};
	
	maze[p.row][p.col] = 2;
	push(p);

	while (!is_empty()) {
		p = pop();
		if (p.row == MAX_ROW -1 && p.col == MAX_COL - 1)
			break;
		if (p.col+1 < MAX_COL && maze[p.row][p.col+1] == 0)
			visit(p.row, p.col+1, p);
		if (p.row+1 < MAX_ROW && maze[p.row+1][p.col] == 0)
			visit(p.row+1, p.col, p);
		if (p.col-1 >= 0 && maze[p.row][p.col-1] == 0)
			visit(p.row, p.col-1, p);
		if (p.row-1 >=0 && maze[p.row-1][p.col] == 0)
			visit(p.row-1, p.col, p);
		print_maze();
	}
	if (p.row == MAX_ROW-1 && p.col == MAX_COL-1) {
		printf("(%d,%d)\n", p.row, p.col);
		while (predecessor[p.row][p.col].row != -1) {
			p = predecessor[p.row][p.col];
			printf("(%d,%d)\n",p.row, p.col);
		}
	} else {
		printf("No path !\n");
	}
	return 0;
}

深度优先是一条路走到完, 走不同需要回溯, 倒退回上一步.

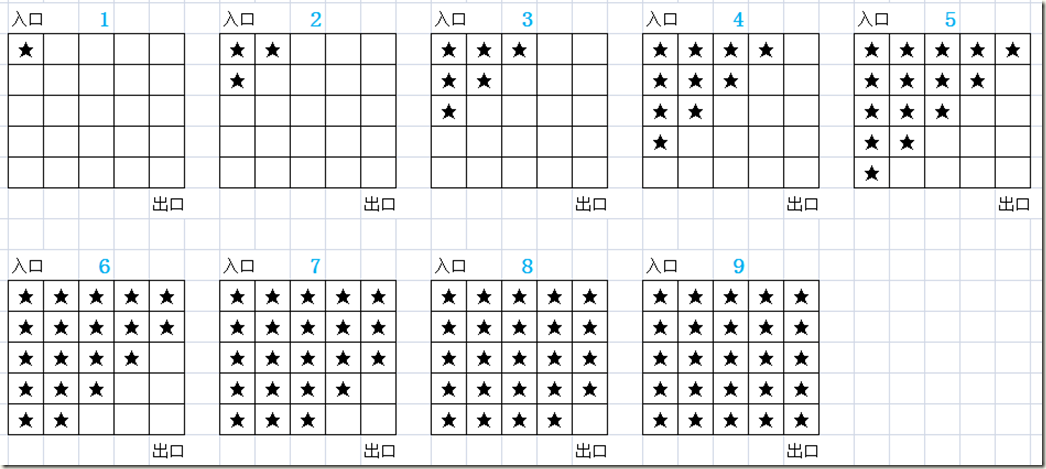
广度优先, 不需要回溯, 也不需要倒退到上一步, 起始说白了, 它不像是一个人在走迷宫, 而是像是N多人, 有分工, 同时尝试多路, 但是一次只能走一步, 所以相比于深度优先, 广度优先算法实现起来, 要简单的多, 如下图:

队列的特点是，先进先出。

队列实现迷宫

队列迷宫/* 
 * sequence implement migong 
 * arthur : kevin
 * date : 2012.09.30
 */

#include <stdio.h>

#define MAX_ROW 5
#define MAX_COL 5

struct point {
	int row, col;
	int predecessor;
} queue[512];
int head = 0, tail = 0;

void enqueue(struct point p)
{
	queue[tail++] = p;
}
struct point dequeue(void)
{
	return queue[head++];
}

int is_empty(void)
{
	return head == tail;
}

/* 1 wall , 0 road */
int maze[MAX_ROW][MAX_COL] = {
	{ 0, 1, 0, 0, 0 },
	{ 0, 1, 0, 1, 0 },
	{ 0, 0, 0, 0, 0 },
	{ 0, 1, 1, 1, 0 },
	{ 0, 0, 0, 1, 0 }
};

void print_maze(void)
{
	int i, j;
	for (i=0; i<MAX_ROW; i++) {
		for (j=0; j<MAX_COL; j++)
			printf("%d ", maze[i][j]);
		putchar('\n');
	}
	printf("*********\n");
}


void visit(int row, int col)
{
	struct point visit_point = { row, col, head-1 };
	maze[row][col] = 2;
	enqueue(visit_point);
}

int main(void)
{
	struct point p = {0, 0, -1};
	
	maze[p.row][p.col] = 2;
	enqueue(p);

	while (!is_empty()) {
		p = dequeue();
		if (p.row == MAX_ROW -1 && p.col == MAX_COL - 1)
			break;
		if (p.col+1 < MAX_COL && maze[p.row][p.col+1] == 0)
			visit(p.row, p.col+1);
		if (p.row+1 < MAX_ROW && maze[p.row+1][p.col] == 0)
			visit(p.row+1, p.col);
		if (p.col-1 >= 0 && maze[p.row][p.col-1] == 0)
			visit(p.row, p.col-1);
		if (p.row-1 >=0 && maze[p.row-1][p.col] == 0)
			visit(p.row-1, p.col);
		print_maze();
	}
	if (p.row == MAX_ROW-1 && p.col == MAX_COL-1) {
		printf("(%d,%d)\n", p.row, p.col);
		while (p.predecessor != -1) {
			p = queue[p.predecessor];
			printf("(%d,%d)\n",p.row, p.col);
		}
	} else {
		printf("No path !\n");
	}
	return 0;
}