结对人员:韩雪东,高扬
一、设计思路
对于大数溢出问题开始很迷茫,不大懂该干什么,思路匮乏。因为只要溢出这个数就不会被存储被改变,这样导致很难去判断溢出后该怎样做,但后来我们改变了一下思路,采用逆向思维,首先找到能存储的最大数,用它来减去将要运行的数,从而与即将要加的数比较,如果小了咋说明相加后会产生溢出,直接结束程序。
二、源代码
// ceshi.cpp : Defines the entry point for the console application. //作者:韩雪东,高扬 //时间:2015/3/29 //#include "stdafx.h" #include "stdio.h" #include "stdlib.h" #include "time.h" int shuchu(int m[],int szcdx,int xhy)//m[]表示要测试的数组,szchx表示数组长度,xhy表示循环条件 { int t,p; int max,sum; //缓存数组赋值 int c[10]; int v[10]; for(t=szcdx-xhy-1;t<szcdx;t++) { c[t-szcdx+xhy+1]=m[t]; } //循环 for(t=xhy;t>=0;t--) { sum=0; for(p=0;p<=t;p++) { if(2147483647-sum<c[p]) { printf(" 数值过大 "); system("PAUSE"); } sum=sum+c[p]; } v[t]=sum; } //循环输出最大值 max=v[0]; for(t=0;t<xhy+1;t++) { if(max<=v[t]) { max=v[t]; } printf(" %d ",v[t]); } return max; } int main(int argc, char* argv[]) { srand(time(NULL)); int a[10]; for(int j=0;j<10;j++) { a[j]=rand()%100000+20000000; } int maxx[10]; for(int i=9;i>=0;i--) { printf("包含数组中第%d个数在内的所有相邻子数组的和:",10-i); maxx[i]=shuchu(a,10,i); printf("\n%d\n\n",maxx[i]); } int maxxx=maxx[0]; for(i=0;i<10;i++) { if(maxxx<=maxx[i]) { maxxx=maxx[i]; } } printf("\n\n该数组的所有子数组的和的最大值:%d\n\n",maxxx); return 0; }
三、结果截图
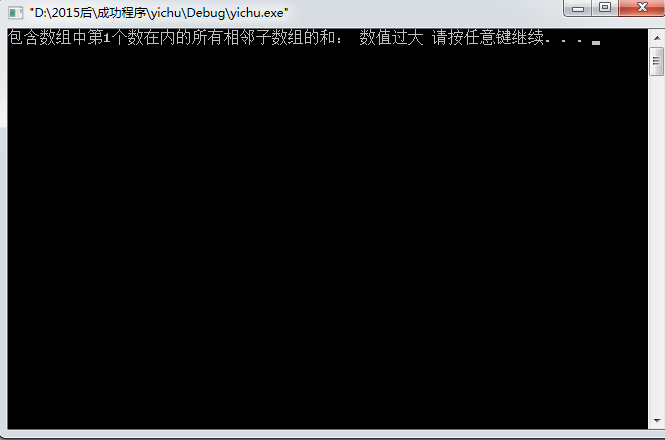

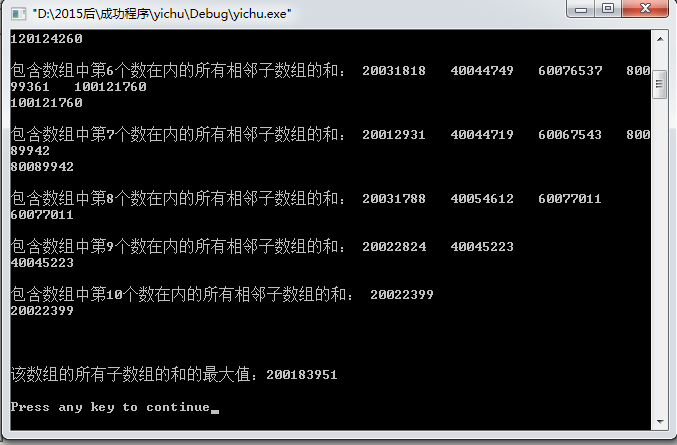
四、心得体会
这是老师对我们程序完善性的考验,以前基本没有考虑过这种情况,我想我们的思路可能存在着漏洞,但这是我们两个人经过很长时间讨论,网上查资料,最后的结果,即使不怎么好,但也是我们共同努力的结果,值了。
五、附图







 本文详细介绍了如何通过逆向思维解决大数溢出问题,包括设计思路、源代码实现及运行结果分析。作者韩雪东和高扬分享了他们从困惑到最终解决的过程,强调了程序完善性和团队合作的重要性。
本文详细介绍了如何通过逆向思维解决大数溢出问题,包括设计思路、源代码实现及运行结果分析。作者韩雪东和高扬分享了他们从困惑到最终解决的过程,强调了程序完善性和团队合作的重要性。
















 943
943

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








