中间人把戏

1.设向量$(x_1,x_2)$,以及向量$(x_1+\Delta x_1,x_2+\Delta x_2)$.则
$$
(x_1+\Delta x_1,x_2+\Delta x_2)-(x_1,x_2)=[(x_1+\Delta x_1,x_2+\Delta x_2)-(x_1,x_2+\Delta x_2)]+[(x_1,x_2+\Delta x_2)-(x_1,x_2)]
$$

2.设向量$(x_1,x_2,x_3)$,以及向量$(x_1+\Delta x_1,x_2+\Delta x_2,x_3+\Delta x_3)$.则
\begin{align*}
(x_1+\Delta x_1,x_2+\Delta x_2,x_3+\Delta x_3)-(x_1,x_2,x_3)&=[(x_1+\Delta x_1,x_2+\Delta x_2,x_3+\Delta x_3)-(x_1,x_2+\Delta x_2,x_3+\Delta x_3)]\\&+(x_1,x_2+\Delta x_2,x_3+\Delta x_3)-(x_1,x_2,x_3)
\end{align*}

下面来看$(x_1,x_2+\Delta x_2,x_3+\Delta x_3)-(x_1,x_2,x_3)$.由于$x_1$已经不变，因此只用处理$x_2,x_3$,而这是1的情形.因此

\begin{align*}
(x_1+\Delta x_{1},x_2+\Delta x_2,x_3+\Delta x_3)-(x_1,x_2,x_3)&=[(x_1+\Delta x_1,x_2+\Delta x_2,x_3+\Delta x_3)-(x_1,x_2+\Delta x_2,x_3+\Delta x_3)]\\&+[(x_1,x_2+\Delta x_{2},x_3+\Delta x_3)-(x_1,x_2,x_3+\Delta x_3)]\\&+[(x_1,x_2,x_3+\Delta x_3)-(x_1,x_2,x_3)]
\end{align*}

下面我们看向量$(x_1,x_2,x_3,\cdots,x_n)$，以及向量$(x_1+\Delta x_1,x_2+\Delta x_2,x_3+\Delta x_3,\cdots,x_n+\Delta x_n)$.

\begin{align*}(x_1+\Delta x_1,\cdots,x_n+\Delta x_n)-(x_1,\cdots,x_n)&=[(x_1+\Delta x_1,\cdots,x_n+\Delta x_n)-(x_1,\cdots,x_n+\Delta x_n)]+[(x_1,\cdots,x_n+\Delta x_n)-(x_1,\cdots,x_n)]\end{align*}

这样子，我们就把情形化作了

$$(x_1,x_2+\Delta x_2,x_3+\Delta x_3,\cdots,x_n+\Delta x_n)-(x_1,x_2+\Delta x_2,x_3+\Delta x_3,\cdots,x_n)$$的情形.而这个情形已经解决.

 

中间人技巧的意义:

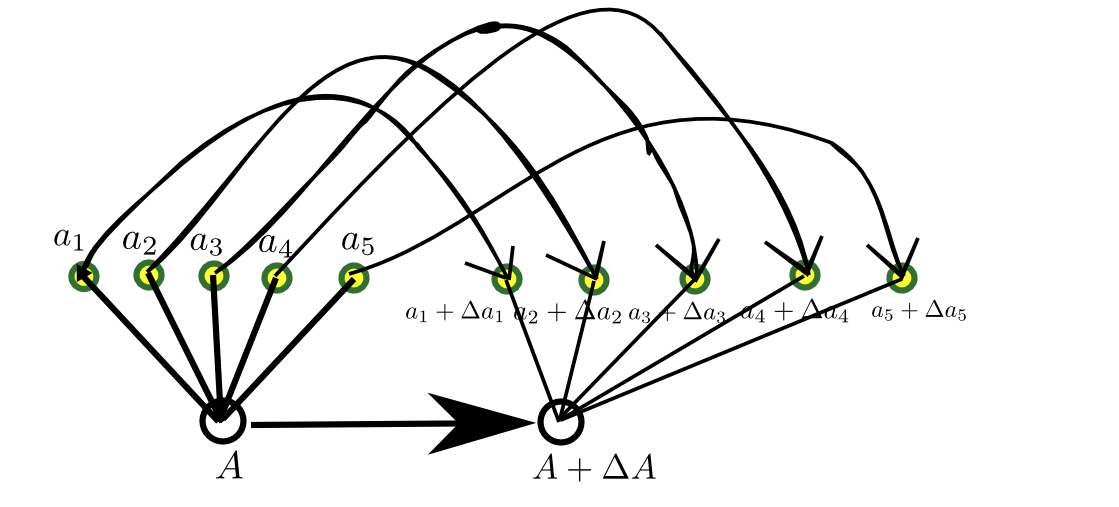
设$A=(a_1,\cdots,a_n)\in\mathbf{R}^n$,$A+\Delta A=(a_1+\Delta a_1,\cdots,a_n+\Delta a_n)\in\mathbf{R}^n$.用图像形象表示如下:

 

 

我们知道，当$A+\Delta A$变成$A$时，$a_1+\Delta a_1,\cdots,a_n+\Delta a_n$是肯定要变成$a_1,\cdots,a_n$.只不过，中间人把戏 让我们把这个变的过程分成$n$步,每次都保持其余的不变，而只让一个变.当这个变完了之后，就放着不动，而让下一个继续变下去.直到$n$次之后，全变完为止.

 

转载于:https://www.cnblogs.com/yeluqing/archive/2012/10/17/3827900.html