HOJ[Hit] 1867

 经理的烦恼

题型：树状数组

描述：1.一列数，第k个数加上x，2.询问[a,b]区间内是素数的个数。

思路：树状数组解决，f[]保存数的值，tree[]保存结点，操作一进行 update()，操作二进行sum();

心得：此题死在了判素数上，0，1没有处理。

 

关于树状数组更深的一点理解：

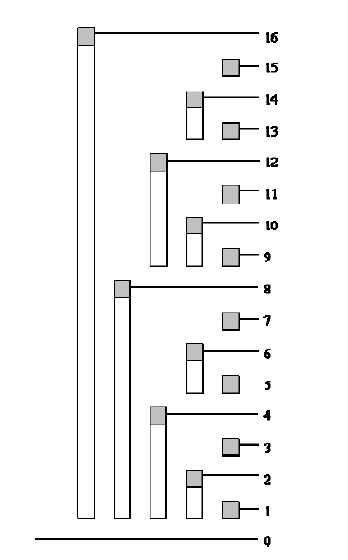
[1].每个idx控制的范围是range = idx&(-idx). 即:idx - range+1~idx

[2].求和，比如:sum(14), 要求出f[1]+..+f[14]，(14)₁₀ = (1110)₂, 14控制2个(10)tree[14] = f[14]+f[13],

去掉14最右边的1，(12)₁₀ = (1100)₂, 12控制4个(100),tree[12] = f[12] + f[11] + f[10] + f[9],

去掉12最右边的1，(8)₁₀ = (1000)₂, 8控制8个(1000),tree[8] = f[8] + ... + f[1].

[3].更新，比如:update(5), 要考虑idx被控制的范围, 即:5(101), 6(110), 8(1000), 16(10000), 每次在最右边的1的位置加上1。

 

 

代码

#include < stdio.h >
#include < math.h >
#include < string .h >
#define LL int
#define NL2 1000001
#define NL1 4000

bool fg[NL1];
int prim[NL1 / 9 ], npm, c;
LL f[NL2];
int tree[NL2];

void getPm()
{
memset(fg, 0 , sizeof (fg));
int i, j;
fg[ 0 ] = fg[ 1 ] = 1 ;
for (i = 2 ; i < NL1; i ++ ) {
if ( ! fg[i]) {
j = i * i;
while (j < NL1) {
fg[j] = 1 ;
j += i;
}
}
}
npm = 0 ;
for (i = 2 ; i < NL1; i ++ )
if ( ! fg[i]) {
prim[npm ++ ] = i;
}
}

bool isprim( int m)
{
int i;
if (m < NL1) {
if ( ! fg[m]) return true ;
else return false ;
} else {
int k = ( int )sqrt(m * 1.0 );
for (i = 0 ; prim[i] <= k; i ++ ) {
if (m % prim[i] == 0 ) return false ;
}
return true ;
}
}

void update( int idx, int k)
{
while (idx <= c) {
tree[idx] += k;
idx += idx & ( - idx);
}
}

int Sum( int idx)
{
int sum = 0 ;
while (idx > 0 ) {
sum += tree[idx];
idx -= idx & ( - idx);
}
return sum;
}

int main()
{
int n, m, cs = 1 ;
int p, i, i0, j0;
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
getPm();
while (scanf( " %d%d%d " , & c, & n, & m) != EOF) {
if ( ! c && ! n && ! m) break ;
printf( " CASE #%d:\n " , cs ++ );
int flg = 0 ;
if (isprim(m)) flg = 1 ;
for (i = 1 ; i <= c; i ++ ) {
f[i] = m;
tree[i] = (i & ( - i)) * flg; //
}
while (n -- ) {
scanf( " %d%d%d " , & p, & i0, & j0);
if (p) {
printf( " %d\n " , Sum(j0) - Sum(i0 - 1 ));
} else {
int t1 = isprim(f[i0]);
f[i0] += j0;
int t2 = isprim(f[i0]);
if (t1 ^ t2) {
if (t1) update(i0, - 1 );
else update(i0, 1 );
}
}
}
puts( "" );
}
return 0 ;
}

转载于:https://www.cnblogs.com/superbin/archive/2010/07/20/1781065.html