吴恩达深度学习专项课程2学习笔记/week1/Setting up optimization problem

Setting up your optimization problem

Normalizing inputs（归一化输入）

归一化输入是可以减速训练的一种方法，包括两步：

1. 均值归零 \[ \mu = \frac{1}{m}\sum_{i=1}^{m}{x^{(i)}}\] \[x := x - \mu \]
2. 方差归一化 \[\sigma^2 = \frac{1}{m}\sum_{i=1}^{m}{x^{(i)}}**2\] \[ x := x / \sigma^2\]

其中“**2”表示逐个元素取平方。
变化过程可以参照下面的例子，相当于通过平移把输入的中心放到原点，在通过缩放使各个维度的范围大体一致。

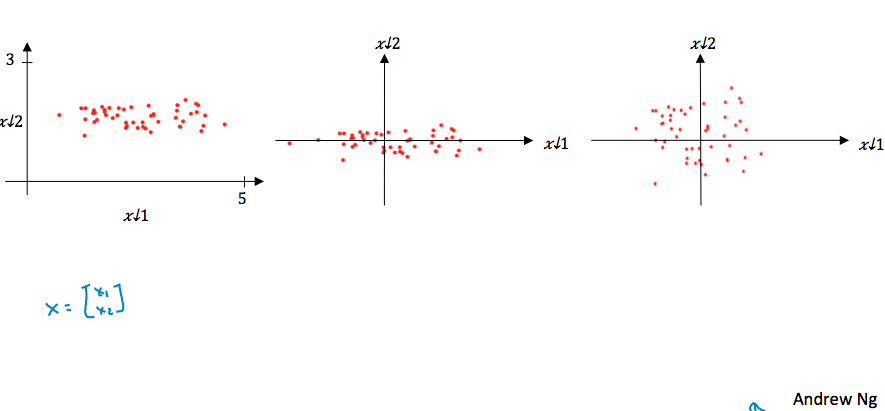
一个提示：如果对训练集进行了归一化，那么对dev/test集也要用同样的\(\mu\)和\(\sigma^2\)进行归一化，因为对所有的数据都要进行一致的变换。

为什么要进行归一化呢？

当不同维度的输入值的范围差别很大时，比如一个是0~1，一个是1~1000，如果不归一化，代价函数（以三维为例，如下图）很可能看起来就像一个扁长的碗，这时梯度下降法去寻找最小值时，学习率的值只能取比较小，需要反复辗转很多步才能取得最小值。归一化以后，会获得更加对称的代价函数，这样梯度下降法寻找最小值时候，会减少走弯路，因此更快地获得最小值。

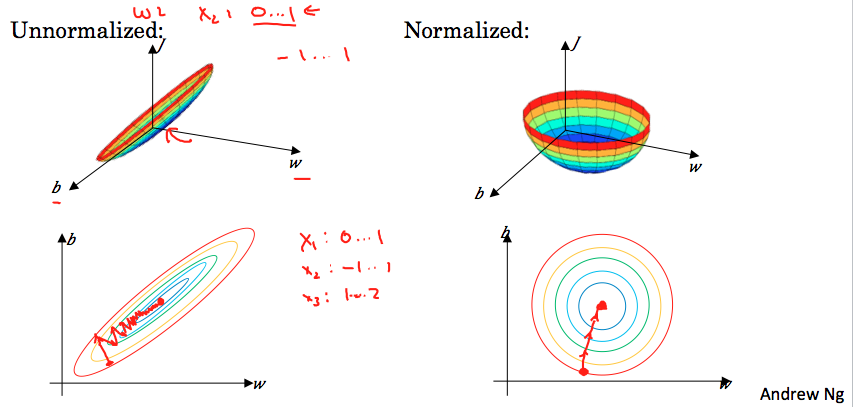
归一化在不同维度的范围差别很大时的效果更明显，但是它一般没有什么坏处，所以在不确定时候，可以始终先进行一下归一化。

Vanishing/Exploding gradients（梯度消失/爆炸）

当训练尤其比较深的网络时，可能需要梯度消失/爆炸的问题。因为每一层的权重值累乘起来的话，如果每层权值略小于单位矩阵，当层数很多时权值就会变得很小（梯度消失，这时梯度下降的每一步都只能走很小很小，学习非常缓慢）；如果每层权值略大与单位矩阵，当层数很多时就会变得很大（梯度爆炸）。

事实上这个问题曾一度是深度学习的壁垒，那么如何解决呢？

Xavier初始化可以缓解梯度消失/爆炸的问题，使赋给权值的初始值不会太大也不会太小，使梯度的变化减缓。

• 激活函数为Relu时 \(W^{[l]}\) = np.random.randn(shape...)*np.sqrt(\(\frac{2}{n^{[l-1]}}\))
• 激活函数为tahn时 \(W^{[l]}\) = np.random.randn(shape...)*np.sqrt(\(\frac{1}{n^{[l-1]}}\))
• 还有其他的版本中，使用的是\(W^{[l]}\) = np.random.randn(shape...)*np.sqrt(\(\frac{2}{n^{[l-1]}+n^{[l]}}\))

这些公式都基于一些统计等理论证明，它们给出了权重比较好的开始的默认值。也可以设置一个超参数，与这些公式相乘去调优，不过一般不会优先去调整这个超参数，但有时它也可以起到一些作用。

（未完待续）

转载于:https://www.cnblogs.com/surimj/p/8405437.html