极限和连续 limits + Continue

上一节我们将导数定义为切线的斜率，这是一种几何解释。我们求出了1/x的斜率为 -1/x² 求出了 f(x) = xⁿ 的斜率是 f^”(x) = n*x^n-1  这些几何的推导都是根据y-y₀  = k * ( x - x₀ ).得来的。

这一节我们重新审视 何是导数？我们将导数定义为变化率。

当做图  y = f（x）的时候我们可以从变化率的角度而言记录x以及y的变化。也就是记录了平均相对变化率 => Δx/Δy，这是一种平均变化。 通常我们可以将x当成时间，这时候y就可以当成另一种变化量。这时候其极限（Δx -> 0）就可以表示为 dy/dx。因此前面的是平均变化率，这个是瞬时变化率。

这里我们举两个栗子（关于变化率的栗子）：

　　　　　　　　

先说第二个，这个比较简单，主要用了高中物理 h= g*t² + v*t.  假设一个人站在教学楼上面向一片草地上扔一个南瓜（Pumpkin drop 南瓜坠游戏），楼的高度为80m ， 由此可得高度随时间的变化公式为 h = 80 - 5*t² 所以当 t = 0 则 h = 80。当t = 4 则 h =0 所以Ave speed ： Δh/Δt = (0-8)/(4-0) 这个是平均速度 下面我们讲一下瞬时速度。 dh/dt = 我们可以根据上一节我们得到的公式 (xⁿ )^” = n*x^n-1  来对这个公式进行求导。dh/dt = 0 - 10*t . 所以当t = 0 则 h“ = 0，当t = 4 则h” =40 。 所以当落地的时候速度为40。这是平均速度的二倍。

 下面说第三个例题。

T = temperature    dt/dx = temperature-gradient 温度梯度

 下面说第四个 sensitivity of measurement 测量灵敏度

 

上述就是导数的介绍，导数的介绍到这里也就完了。

---

 

下面开始对导数进行详细的介绍。

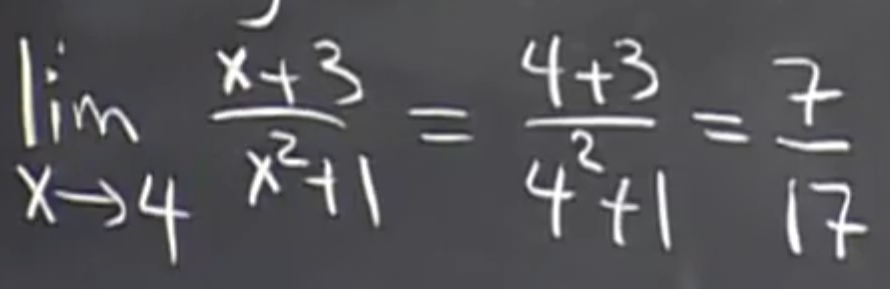简单的极限如下： 十分简单，这个是简单极限。

 

左极限和右极限。

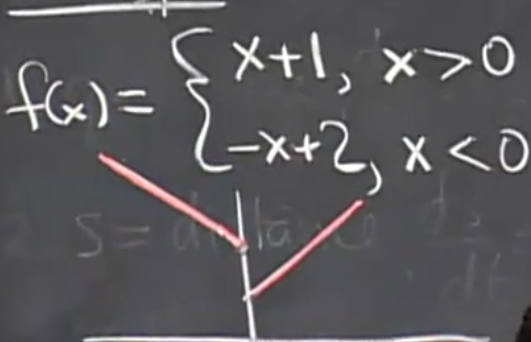（图中和y轴相交的两点需要用一个园扩起来，表示不包含这一点。）对这一题进行求左右极限得 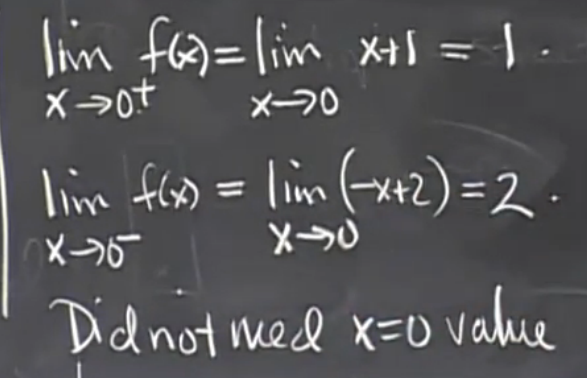：  求极限不需要知道 x = 0的值 。

 

 下面我们定义什么是连续。

   如果X₀需要满足连续条件的化，则他需要满足一下几个条件。

 1：极限必须存在。在上例中就是当 x = 0 的时候 f（x）必须由确定的值。

 2：左右极限必须相等，上一个例题就不符合这一点。

 

下面看一些不连续的函数。

　间断跳跃

　　　　1：左右极限均存在但是不相等。就是我们上面的那个栗子。

　可去间断

　　　　1：左右极限存在且相等 

 一条直线的中间有一个洞。丢的那一点可能在那个洞的正上，下方。当我们重新定义这一点的时候，直线可以连续，所以这就是可去间断点。 。

开始举栗子：

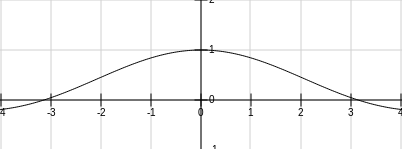h(x) =sin ( x ) / x 的图形如下。 通过图形可得  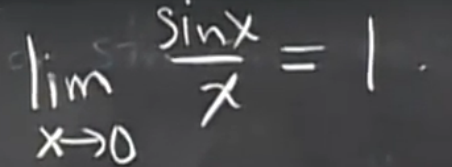 当 x = 0 的时候 该点是没有对应的值得 。 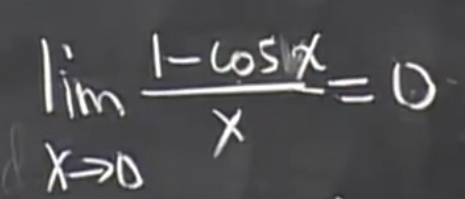这两个都是 “ 可去间断点 ” 。

 

无穷间断

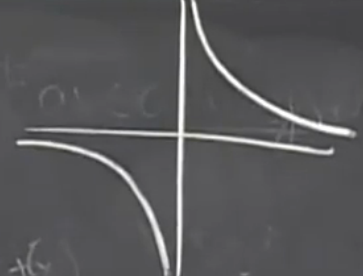y = 1/x 的图形 这里要分左右连续。我们可以得到他的左右极限为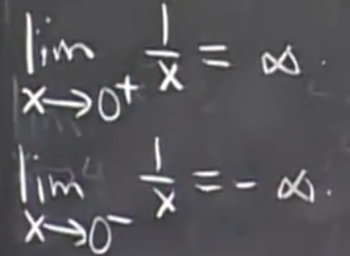： 如果我们部分左右极限直接让他为正无穷或者负无穷的化，这是十分扯淡的盲人摸象。

 

其他（丑陋）间断。

　　y = sin（1/x）他没有极限属于其他间断。

定理：可导必连续，若f在x处可导，那么该图像在x处必然连续。

 对其进行证明假设f（x）在x₀处可导那么问其是否连续。

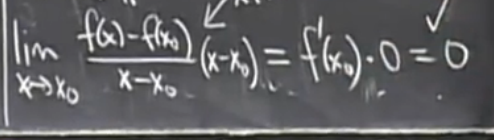　　    f(x₀) = (f(x)-f(x₀))/(x-x₀)

 

转载于:https://www.cnblogs.com/A-FM/p/6275038.html