数据结构 - 树

数据结构 - 树

 

一、索引

---

概念：在关系型数据库中，索引是一种单独的、物理的对数据表中一列或多列的值进行排序的一种存储结构，它是某个表中一列或若干列值的集合和相应的指向表中物理标识这些值得数据页的逻辑指针清单。索引的作用相当于图书的目录，可以根据目录中的页码快速找到所需的内容。

二、索引分类

---

分类：分区和非分区索引、常规B树索引、位图索引、翻转索引等。其中，B树索引属于最常见的的索引。

 

三、BTree和B+Tree

---

B树又叫做平衡多路查找树，这里的B是Balance的意思。

树的高度：表示树从根节点开始一共有几层（注意：从0还是1开始数）。

• 一棵含有N个总关键字数的m阶B树的最大高度是多少？
• 答案：log(ceil(m/2))(N+1)/2 + 1

树的阶：表示每个节点最多有几棵子树（注意：根节点至少有2棵，除非是叶子节点）。

 

B树特性如下：

1. 每个节点最多含有 m 个叶子结点；
2. 非叶子节点（根节点除外）至少要有[ceil(m/2)]个叶子节点；
3. 当根节点不是叶子节点时，至少要有2个叶子节点；
4. 非叶子节点有 k 个叶子结点与 k - 1 个关键字；
5. 任何叶子节点都在同一层，并且叶子节点不包含任何关键字信息；

 

四、B树插入操作

---

要求：需要在一个高度为 h 的 m 阶B树中插入相应关键字。

假设 m 等于 k ，任意节点最多有 k 个叶子节点与 k - 1个关键字。

1. 若该节点的关键字个数小于 k - 1，则直接插入；
2. 若该节点的关键字个数等于 k - 1，则该节点分裂；
3. 重复上述工作；

节点分裂：以中间元素为界，将一半关键字分裂到右节点中，中间元素上移到父节点中。

 

举个例子：C N G A H E K Q M F W L T Z D P R X Y S

1、下图表示一棵5阶的B树，叶子结点 MAX = 5，关键字 MAX = 4。

插入后元素：H E K Q M F W L T Z D P R X Y S

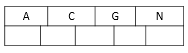
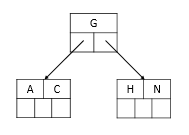
2、插入H，由于要满足 K <= m - 1，由于空间不足需要将节点进行分裂。

分裂过程中，节点分裂为两个，关键字 H 排在 G 的后面，G作为中间元素上移到父节点，成为新的根节点。

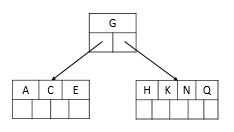
插入后元素：E K Q M F W L T Z D P R X Y S

3、插入E、K、Q，由于节点增多，关键字的插入不会导致分裂。

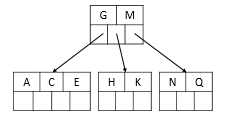
插入后元素：M F W L T Z D P R X Y S

4、插入M，按照顺序需要放入右边树中，由于空间不足需要将节点进行分裂。

分裂过程中，节点分裂为两个，关键字 M 排在 N 的前面，M作为中间元素上移到父节点。

插入后元素：F W L T Z D P R X Y S

5、插入F、W、L、T，由于节点增多，关键字的插入不会导致分裂。

插入后元素：Z D P R X Y S

 

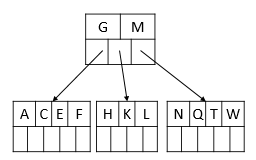
6、插入Z，按照顺序需要放入右边树中，由于空间不足需要将节点进行分裂。

分裂过程中，节点分裂为两个，关键字 Z 作为最后一个字母，T作为中间元素上移到父节点。

插入后元素：D P R X Y S

 

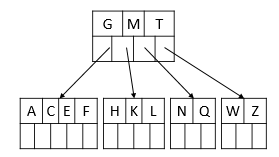
7、插入D，按照顺序需要放入左边树中，由于空间不足需要将节点进行分裂。

分裂过程中，节点分裂为两个，关键字 D 排在 C 后面，D作为中间元素上移到父节点。

插入后元素：P R X Y S

 

 

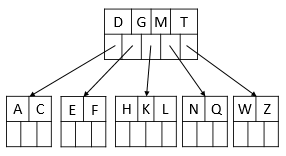
8、插入P、R、X、Y，由于节点增多，关键字的插入不会导致分裂。

插入后元素：S

 

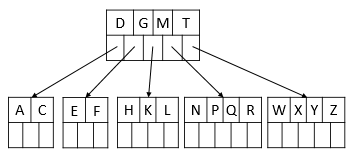
 9、插入S，按照顺序需要放入第四棵树，由于空间不足需要将节点进行分裂。

分裂过程中，节点分裂为两个，关键字 S 排在 R 后面，Q作为中间元素上移到父节点。

由于父节点空间不足，导致根节点也要进行分裂。关键字 Q 在 M 后面，M 作为中间元素上移到父节点。

因此，关键字 M 成为新的根节点。

 

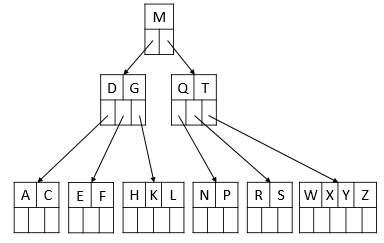
五、B树删除操作

---

要求：需要在一个高度为 h 的 m 阶B树中删除相应关键字。

假设 m 等于 k ，任意节点最多有 k 个叶子节点与 k - 1个关键字。

1. 在树中查找被删除关键字K所在的位置；
2. 进行删除K的操作；

若被删关键字K所在的节点非叶子节点，则用K的中序前驱或后继K’取代K，然后从叶子中删除K’。

从叶子节点开始删关键字K的三种情形：

情形一：

情形二：

情形三：

 

 

1. 若该节点的关键字个数大于ceil(m/2) - 1，则直接删除；
2. 若该节点的关键字个数小于等于ceil(m/2) - 1，则需要向其父节点借关键字来满足条件；
3. 重复上述工作；

节点合并：

以中间元素为界，将一半关键字分裂到右节点中，中间元素上移到父节点中。

 

举个例子：在下列B树中依次删除 H、T、R、E关键字。

1、删除关键字 H，由于关键字 H 所在的节点满足ceil(m/2) - 1 = 2条件，直接删除。

删除后元素：T R E

 

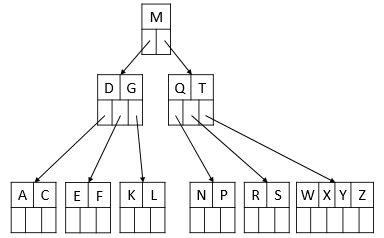
2、删除关键字 T，由于关键字 H 所在的节点满足ceil(m/2) - 1 = 2条件，直接删除。

删除后元素：T R E

 

转载于:https://www.cnblogs.com/randyma/p/6951043.html