canvas曲线面片2

最新推荐文章于 2022-05-22 09:39:22 发布
转载 最新推荐文章于 2022-05-22 09:39:22 发布 · 108 阅读 · 0 ·
CC 4.0 BY-SA版权
原文链接：http://www.cnblogs.com/daidaidai/p/5525582.html

写前面

 

此篇的妹妹篇 是canvas曲面面片1 如果你没看 可以去了解下

在前面那篇 我们用了 双线性面片 还记得不？

这篇效果如下

 

 

 

这就是曲线面片的威力！  让这只萌萌の生物动起来了  视线跟随着小球 晃动着脑袋~

用到的是贝塞尔面片 准确的说是二次贝塞尔面片（下面说的都是二次） 当然有高次的 不过一般来说三次就够用了

先讲解下什么是贝塞尔面片 在这之前你得知道啥是贝塞尔曲线 （不懂的先自己找资料了解下）

上篇用到的是线性面片 只要4个控制点就够了 而贝塞尔面片 至少需要用到9个控制点   如图

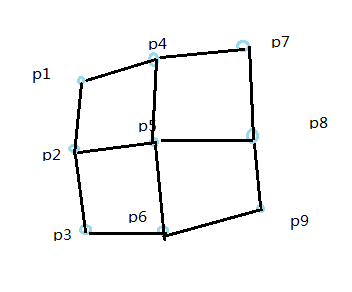
但如何表示出曲面呢？这9个点 其实就可以表示出无线多个贝塞尔曲线了 也就形成了面片

跟上篇一样 可以先黄方向插值 随后蓝方向插值  当然反过处理也是ok的 然后拼接成三角图元就行了

现在是可以表示出曲面了 但是没有贴图 ！ 还记得上篇我们是怎么处理贴图的不？

因为我们上次用的是canvas2d api  所以在处理的时候 对一个三角图元就一个drawImage 然后解线性方程组 算出transform中的矩阵

这篇我用的是webgl 不需要结出矩阵的值了 只要给出纹理坐标就行 但是要注意 webgl坐标系和图片坐标是相反的 ！

 

直接看那部分关键代码吧 如下

可以看到 处理循环中的逻辑和上一篇是差不多的 只是把获取插值坐标函数分离了出来

这里有个maps数组 这个就是存储的纹理坐标了  因为坐标系的原因（相反的） 所以 1-

贝塞尔面片原理大致就是这样了~

 

但那个萌萌の生物是怎么形成的呢？ 这个生物需要很多个面片  看我的img包你就能猜到大概了

我这里用了5张纹理  工厂生成了5个面片对象

光是这样萌萌の生物是不会动的！

还得根据某个坐标（这里是那个小球） 给那些需要偏移的控制点计算位置  如图

 

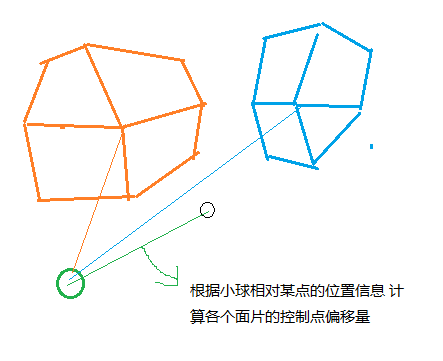
这里的微调工作繁琐到爆炸！如下 各种微调！

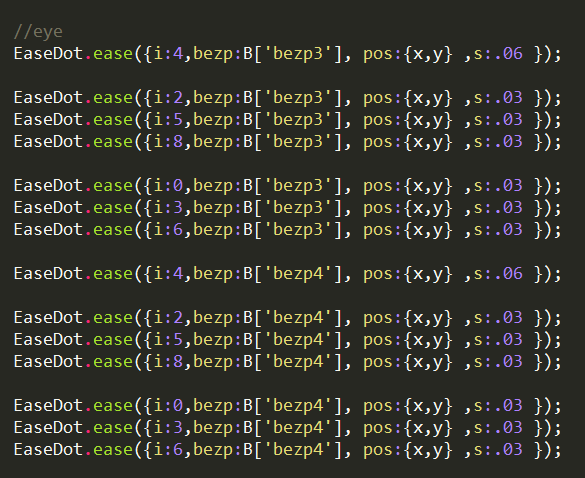
这里花费了我大量的精力 为了就是使面部动作生动 对各个控制点给参数。。各种微调

还有一开始把各个面片合成原始图像的位置 也是各种微调！

 

这玩意儿还是要有个编辑器才行  设定各种终止 初始值 做各种动画插值变换

再对人物细分 如 对眉毛 腮红也单独来个面片  一定会非常nice

不过 现阶段是不打算考虑做编辑器这种事的  这个优先级很后 。。

再说了 市面上应该有这种编辑器的吧（我也不清楚）

最重要的还是实现的思想

 

 

demo源码  用chrome打开  

 

转载于:https://www.cnblogs.com/daidaidai/p/5525582.html

基于canvas绘制多条贝塞尔曲线组成3D双三次曲面片
学以致用 知行合一
05-05 1296
贝塞尔曲面是一种用于计算机图形学、计算机辅助设计和有限元建模的数学样条。与贝塞尔曲线一样，贝塞尔曲面由一组控制点定义。 贝塞尔曲面最常见的用途是作为双三次面片的网络（其中m = n = 3）。因此，单个双三次面片的几何形状完全由一组 16 个控制点定义。这些通常以与贝塞尔曲线连接形成 B 样条曲线类似的方式连接起来形成B 样条曲面。 贝塞尔曲面网格在表示光滑表面方面优于三角形网格。它们需要更少的点（因此更少的内存）来表示曲面，更易于操作，并且具有更好的连续性。此外，其他常......
利用Canvas绘制多条贝塞尔曲线，构建一个3D双次曲面片
MpkeShell的博客
09-27 248
我们将使用HTML5的Canvas元素和JavaScript来实现这个过程Canvas元素和JavaScript来实现这个过程。在绘制曲线之前，我们需要定义一些控制点。接下来，我们将使用JavaScript来获取对Canvas的引用，并设置其上下文为2DCanvas元素和JavaScript来实现这个过程。接下来，我们将使用JavaScript来获取对Canvas元素和JavaScript来实现这个过程。接下来，我们将使用JavaScript来获取对Canvas的引用，并设置其上下文为2D绘图环境。
canvas 曲线面片1
weixin_33937913的博客
04-07 110
写前面 *姐姐篇已完成 传送canvas曲线面片2 (别跟我说这东西没用 并不想理你！) 什么是曲线面片？ 如图 上面这个就是相对简单的双线性面片 可通过4个点来控制 左上角 A点 顺时针依次就是ABCD 这个东西 其实就是BA方向 和 DA 方向的线性插值组合 下图 先沿着DA CB 方向插值 再继续对 BA 方向插值 生成三角坐标的代码： ...
canvas 2d 贴图技术实践
dfpbut5000的博客
07-15 389
　　最近在公司内部的技术协会论坛里闲逛的时候，无意中发现了一篇手淘前端大牛岑安两年前写的博文，讲述了canvas的2d贴图技术。看到后觉得相当神奇。于是就自己实现了一下。不过岑安前辈的那篇博文也只是大概讲述了一下实现思路，整个逻辑还是自己慢慢摸索出来的，过程还是挺心酸的，所以在此记录一下并且分享一下，让跟我一样喜欢canvas的人有所收获吧。 　　废话不说，先把demo贴出来，好歹让大...
html绘制两条直线,HTML5/Canvas数学之美：使用直线绘制多个曲面图形
weixin_39865277的博客
05-31 245
JavaScript语言：JaveScriptBabelCoffeeScript确定(function() {var $canvas = $('.mycanvas');var Shape = function($element, options) {if (!(this instanceof Shape)) {return new Shape($element, options);}this.$c...
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d.art3d import Poly3DCollection # 生成数据 Round = np.array([0, 1, 2]) # 横轴 Round A1 = np.array([2, 4, 6, 8]) # 纵轴 A1 Z = np.array([ [17.1, 22.3, 23.8, 24.1], [14.5, 19.0,20.4, 20.9], [11.8, 15.1, 16.7, 17.3] ]) # 创建图形 X, Y = np.meshgrid(A1, Round) fig = plt.figure(figsize=(8, 6)) ax = fig.add_subplot(111, projection='3d') # 绘制3D曲面 for i in range(Z.shape[0]): # 绘制每个数据线条，并标注关键点 ax.plot(Y[i], X[i], Z[i], '-o') ax.plot(Y[i], X[i], np.zeros_like(Z[i]), color='gray', alpha=0.5) # 填充每个四边形面 for j in range(len(A1) - 1): verts = [ [Y[i, j], X[i, j], 0], [Y[i, j + 1], X[i, j + 1], 0], [Y[i, j + 1], X[i, j + 1], Z[i, j + 1]], [Y[i, j], X[i, j], Z[i, j]] ] ax.add_collection3d(Poly3DCollection([verts], color=plt.cm.viridis(i / len(Round)), alpha=0.4)) # 在每个关键点上添加注释 for j in range(Z.shape[1]): ax.text(Y[i, j], X[i, j], Z[i, j] + 0.03, f'{Z[i, j]:.2f}', color='black', ha='center') # 绘制每个点之间的连接线 for j in range(Z.shape[1]): ax.plot(Y[:, j], X[:, j], Z[:, j], '--', color='gray') # 设置标签 ax.set_xlabel('Round') ax.set_ylabel('A1') ax.set_zlabel('Cooperation Rate') # 显示图像 plt.show() # 绘制无直线3D瀑布图 import matplotlib.pyplot as plt import matplotlib.ticker as ticker from mpl_toolkits.mplot3d.art3d import Poly3DCollection import numpy as np def line_3d(x, y, z, x_label_indexs): """ 在y轴的每个点，向x轴的方向延伸出一个折线面：展示每个变量的时序变化。 x: x轴，时间维，右边。 y: y轴，变量维，左边。 z: z轴，数值维。二维矩阵，y列x行。每一行是对应变量的一个时间序列。 x_label_indexs: 需要标注的时间点。 """ x_num = len(x) y_num = len(y) if z.shape[0] != y_num or z.shape[1] != x_num: return -1 # 制作坐标格点(z中每个点对应的x、y坐标) X, Y = np.meshgrid(x, y) # 初始化 canvas = plt.figure() # 创建画布 axs = canvas.add_subplot(111, projection='3d') # 添加三维子图 # 若把111改成234，则意思是：创建一个2*3的网格，并在第4个格子中创建一个axes # 绘制折线面
最新发布
03-12
2. **面片填充**：使用`Poly3DCollection`时需要提供顶点列表，每个面片由多个多边形组成[^1] 3. **瀑布图核心**： - 通过`fill_between`创建二维填充区域 - 使用`add_collection3d`将二维图形提升到三维空间 - `...
cesium态势标会（闭合曲面）
God's asylum的博客
05-22 1668
vue + cesium绘制闭合曲面标绘与编辑，采用es6模块化写法逻辑清晰，会有明显的标注说明，使代码容易读懂，理解和学习
Unity3d_NGUI和UGUI的学习
lfh719852029的博客
06-26 9043
由于之前刚入门的时候，应Unity3d整体发展的要求我们自学了UGUI(相对来说UGUI比NGUI做得更好一些，后面会有2者对比)，但是后来公司要求使用NGUI，所以我这边把之前学习UGUI（不全，当时资源有限）和NGUI的学习心得什么的整理一下。学习UI，基础差的看一些教程，基础好的可以直接查看官方案例，根据案例上的相关功能自己做，有什么不懂的参数或者小知识网上问一下，向他人请教也是可以的。
多年收集的一些稀有软件4
热门推荐
weixin_33728708的博客
10-06 2万+
QQ:365543212　 Geovariances产品: Geovariances Isatis 2013 1CD(地质统计学软件) Geovariances.Isatis.2016.Win64 1CD Geovariances Minestis 2016 v2.0.0Win64 1CD 　 软脑公司产品: 3D-Sigma for WinALL-ISO 1CD（岩土体三维应力分...
一条神奇的贝塞尔曲线及其应用
程序IT圈
05-24 274
程序IT圈学习编程技术，关注这个公众号足够了今天的主题，就是主要和大家介绍贝塞尔曲线！什么是贝塞尔曲线？贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图...
实时曲线显示 Visual C++实现
09-16
实时曲线显示 Visual C++实现，本源码来自《VC实例精粹》所附光盘，仅供学习研究使用！
使用Canvas + Path和“曲面细分”算法实现钢笔笔锋效果
轮子初级玩家
07-05 8835
本文用于在无法获取压感的设备上实现书法效果，因此所有的书写效果的笔触粗细变化，均是通过速率进行确认。最后实现效果如下（不会书法，只能让大家体会一下效果），代码基于之前的文章https://blog.youkuaiyun.com/cjzjolly/article/details/88661286上进行修改而成： 一、推导： 在正常的情况下，使用Canvas和Path分段绘制用户的书写结果时...
【Qt OpenGL教程】28：贝塞尔曲面
cly116的博客
08-15 1万+
这次教程中，我们将介绍贝塞尔曲面，因此这是关于数学运算的一课（这导致很不好讲），来吧，相信你能搞定它的！这一课中，我们并不是要做一个完整的贝塞尔曲面库（库的话OpenGL已经完成了），而是一个展示概念的程序，来让你熟悉曲面是怎么计算实现的。
三次贝塞尔曲面
qq_39328456的博客
09-16 3715
三次贝尔赛曲面 基于DirectX11的曲面细分章节实现的矩形的三次贝塞尔曲面，特此做下笔记 一个矩阵，可以分为水平方向和垂直方向，分别做贝塞尔曲线。 一个4*4控制点的面片，第i行的贝塞尔曲线函数 通过对每一行的贝塞尔曲线的基础上，对同一列做列贝塞尔曲线，其中控制点p是行贝塞尔曲线的坐标； 将所有列曲线上的顶点求出后，求得到了贝塞尔曲面。 由于并没有新的控制点...
绘制Bezier三角面片
拉风小宇的博客
10-23 3750
将Bezier曲线曲面推广到三角域，得到三角曲面片，用matlab实现
绘制：Canvas的使用、Path基础、Path绘制贝塞尔曲线
m0_38058826的博客
02-20 876
Canvas的使用、Path基础、Path绘制贝塞尔曲线。 一、Canvas回顾 Canvas的使用相对基础一点，我们来一起通过API回顾下： 类别 API 描述 绘制图形 drawPoint, drawPoints, drawLine, drawLines, drawRect, drawRoundRect, drawOval, drawCircle, drawArc ...
Canvas 画贝塞尔曲线（二阶曲线和三阶曲线）
清山博客
01-06 3026
效果图为动态图，一个小圆点沿着曲线运动，并显示实时点坐标。 在线预览： 二阶：http://qingshanboke.com/demo/quadratic.htm 三阶：http://qingshanboke.com/demo/bezier.htm 一、实现思路： 1.用两个canvas实现，一个绘制曲线，一个绘制运动圆点。 2.绘制曲线：可以通过canvas提供的API方法绘制...
利用Canvas技术绘制创新曲线进度条效果
标题中提到的知识点是关于如何使用HTML5的Canvas元素来实现具有曲线效果的进度条。这种进度条可以应用在多种Web界面中，用来展示数据加载、处理进度等信息。下面详细说明相关知识点。 ### Canvas基础 Canvas是...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值