正规矩阵求参数

最新推荐文章于 2024-02-28 09:19:46 发布

weixin_34252686

最新推荐文章于 2024-02-28 09:19:46 发布

阅读量324

点赞数

CC 4.0 BY-SA版权

原文链接：https://my.oschina.net/lvyi/blog/608155

为什么80%的码农都做不了架构师？>>>

已知售卖房屋的参数和出售价格，我们去预测其他房屋时

输入图片说明

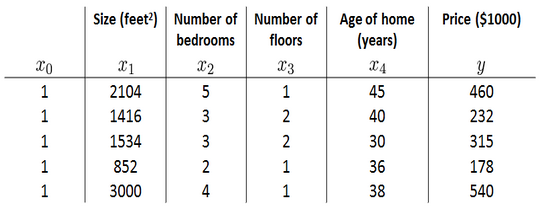
我们会先假设出一个函数能大致拟合这些数据，比如用线性函数

f(X) = θ1X1 + θ2X2 + θ3X3 + θ4X4

或者用非线性的函数

f(X) = θ1log(X)

代价函数由来

这些假设函数的参数都是未知的，怎么去求它们呢？

如果刚好所有的点都满足 f(x) 函数，对于第一个式子显然只需要代入四个点解方程分别求得 (θ1, θ2, θ3, θ4)。对于第二个式子只需任意代入一个点就可以求得参数 θ1。

但这些点都不完全分布在我们的假设函数上，这样就需要给出一个标准来求得最优参数。这就是代价函数(Cost Function)。代价函数表征的是假设函数与真实数据之间的差距，定义为：

输入图片说明

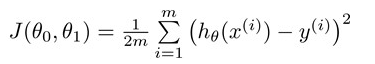
h 是假设函数，y代表真实函数的值。

可以得知，当 J 的值越小，假设函数和真实函数就越接近。

梯度下降法求参数

那么已知了代价函数之后，怎么去确定参数呢。只需要把所有的参数值遍历一遍代入代价函数，最后取代价函数值最小的时候对应的参数即可。

这样做效率很低，所以引入了梯度下降法来加速求解过程。

正规方程法求参数

还有另一种方法可以同样求得这些参数。

Normal equation：Method to solve for θ analytically

正规方程公式：

输入图片说明

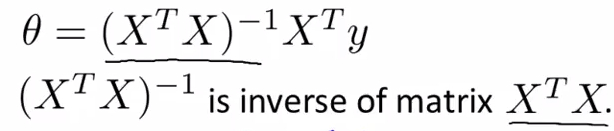
X = [1 2104 5 1 45
     1 1416 3 2 40
     1 1534 3 2 30
     1 852  2 1 36
     1 3000 4 1 38];
Y = [460 232 315 178 540]';
parament = pinv(X'*X)*X'*Y;
disp(parament)

结果

这里求得是 f(X) = θ0X0 + θ1X1 + θ2X2 + θ3X3 + θ4X4 函数的五个参数

若将 X 修改为

X = [1 2104*2104 5 1 45
     1 1416*1416 3 2 40
     1 1534*1534 3 2 30
     1 852*852  2 1 36
     1 3000*3000 4 1 38];
Y = [460 232 315 178 540]';
parament = pinv(X'*X)*X'*Y;
disp(parament)

则求得的是 f(X) = θ0X0 + θ1X1*X1 + θ2X2 + θ3X3 + θ4X4 函数的五个参数

转载于:https://my.oschina.net/lvyi/blog/608155