吴恩达深度学习笔记1-神经网络的编程基础(Basics of Neural Network programming)

一：二分类(Binary Classification)

　　逻辑回归是一个用于二分类(binary classification)的算法。在二分类问题中，我们的目标就是习得一个分类器，它以对象的特征向量作为输入，然后预测输出结果?为 1 还是 0。

符号定义 ：

?：表示一个??维数据，为输入数据，维度为(??,1)； 

?：表示输出结果，取值为(0,1)； 

(?(?),?(?))：表示第?组数据，可能是训练数据，也可能是测试数据，此处默认为训练数
据；

? = [?(1),?(2),...,?(?)]：表示所有的训练数据集的输入值，放在一个 ?? × ?的矩阵中，
其中?表示样本数目;

? = [?(1),?(2),...,?(?)]：对应表示所有训练数据集的输出值，维度为1 × ?。 

 

二：逻辑回归(Logistic Regression) 

　　下图是 sigmoid 函数的图像，如果我把水平轴作为?轴，那么关于?的 sigmoid 函数是这样的，它是平滑地从 0 走向 1，让我在这里标记纵轴，这是 0，曲线与纵轴相交的截距是 0.5，这就是关于?的 sigmoid 函数的图像。我们通常都使用?来表示??? + ?的值。

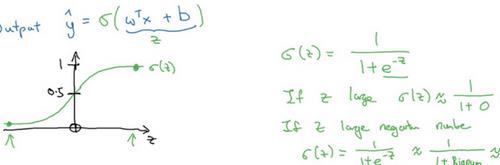
关于 sigmoid函数的公式是这样的，

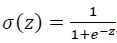
　　当你实现逻辑回归时，你的工作就是去让机器学习参数?以及?这样才使得? ^成为对? = 1这一情况的概率的一个很好的估计。在符号上要注意的一点是当我们对神经网络进行编程时经常会让参数?和参数?分开，在这里参数?对应的是一种偏置。

　　为了训练逻辑回归模型的参数参数?和参数?我们，需要一个代价函数，通过训练代价函数来得到参数?和参数?。先看一下逻辑回归的输出函数：

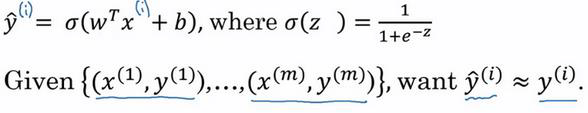
　　为了让模型通过学习调整参数，你需要给予一个?样本的训练集，这会让你在训练集上找到参数?和参数?,，来得到你的输出。对训练集的预测值，我们将它写成? ^，我们更希望它会接近于训练集中的?值。

下面介绍损失函数，损失函数又叫做误差函数，用来衡量算法的运行情况，Loss function:?(? ^,?). 

　　我们通过这个?称为的损失函数，来衡量预测输出值和实际值有多接近。一般我们用预
测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为
当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部
最优值，梯度下降法很可能找不到全局最优值，虽然平方差是一个不错的损失函数，但是我
们在逻辑回归模型中会定义另外一个损失函数。我们在逻辑回归中用到的损失函数是：

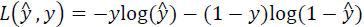
　　当? = 1时损失函数? = −log(? ^)，如果想要损失函数?尽可能得小，那么? ^就要尽可能大，
因为 sigmoid 函数取值[0,1]，所以? ^会无限接近于 1。
　　当? = 0时损失函数? = −log(1 − ? ^)，如果想要损失函数?尽可能得小，那么? ^就要尽可
能小，因为 sigmoid 函数取值[0,1]，所以? ^会无限接近于 0。

　　在这门课中有很多的函数效果和现在这个类似，就是如果?等于 1，我们就尽可能让? ^变
大，如果?等于 0，我们就尽可能让 ? ^ 变小。 损失函数是在单个训练样本中定义的，它衡
量的是算法在单个训练样本中表现如何，为了衡量算法在全部训练样本上的表现如何，我们
需要定义一个算法的代价函数，算法的代价函数是对?个样本的损失函数求和然后除以?:

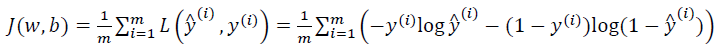
　　损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价，所以在训练逻
辑回归模型时候，我们需要找到合适的?和?，来让代价函数 ? 的总代价降到最低。 根据我
们对逻辑回归算法的推导及对单个样本的损失函数的推导和针对算法所选用参数的总代价
函数的推导，结果表明逻辑回归可以看做是一个非常小的神经网络。

 

三：梯度下降法（Gradient Descent） 

梯度下降法可以做什么？
在你测试集上，通过最小化代价函数（成本函数）?(?,?)来训练的参数?和?，

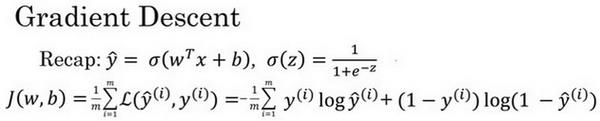
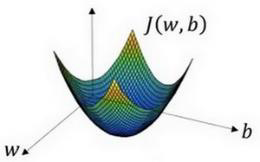
　　在上图中，横轴表示空间参数?和?，在实践中，?可以是更高的维度，但是为了
更好地绘图，我们定义?和?，都是单一实数，代价函数（成本函数）?(?,?)是在水平轴?和
?上的曲面，因此曲面的高度就是?(?,?)在某一点的函数值。我们所做的就是找到使得代价
函数（成本函数）?(?,?)函数值是最小值，对应的参数?和?。

　　假定代价函数（成本函数） ?(?) 只有一个参数?，即用一维曲线代替多维曲线，这样可
以更好画出图像。

                   

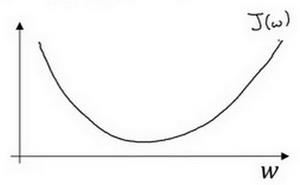
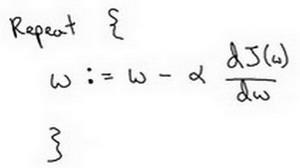
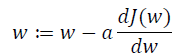
迭代就是不断重复做如图的公式:
:=表示更新参数,

　　? 表示学习率（learning rate），用来控制步长（step），即向下走一步的长度 ??(?) ??
就是函数?(?)对? 求导（derivative），在代码中我们会使用??表示这个结果。

梯度下降法的细节化说明（两个参数）
逻辑回归的代价函数（成本函数）?(?,?)是含有两个参数的。

 

转载于:https://www.cnblogs.com/sl0309/p/10786303.html