洛谷 1736 创意吃鱼法

看看题目

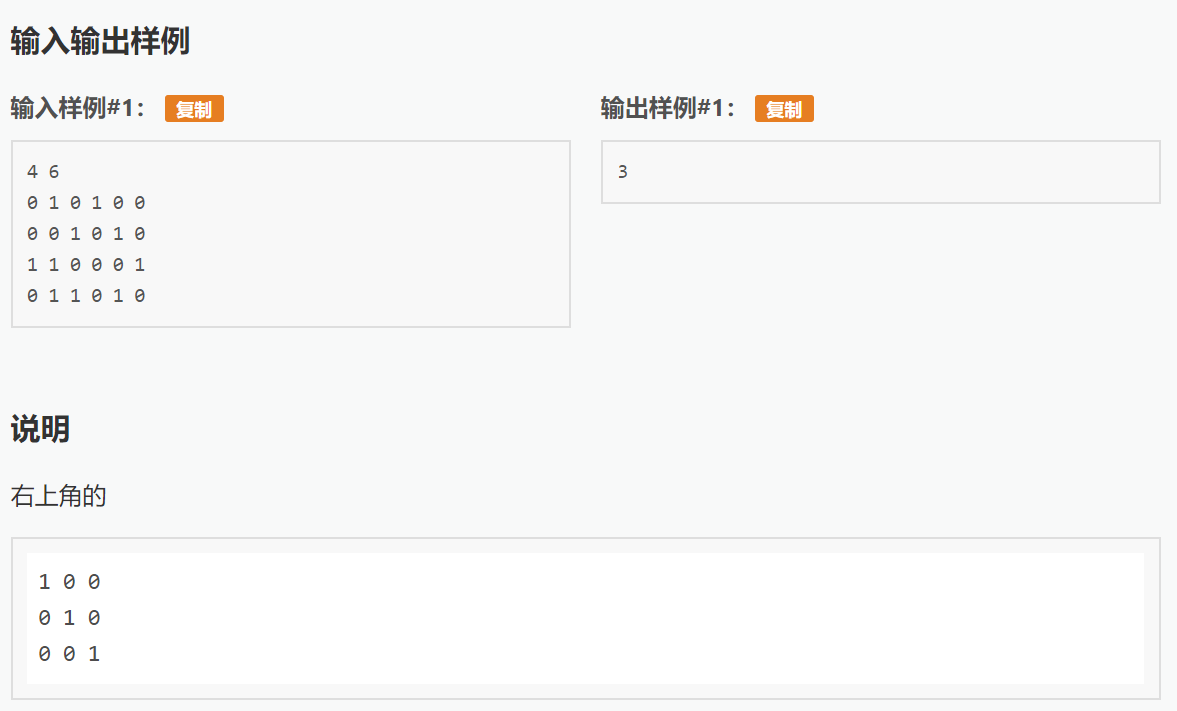
这题的意思是找一个正方形，使得对角线最长，并且除了对角线上是1，正方形的其他区域都为0

是不是很像P1387 最大正方形这题

我们分析一下

要使这个正方形方向只有对角线上有1其他都为0

我们可以维护一个二维的前缀和来表示某一方向上最长的连续为0的长度

dp方程如下

向右下方斜着的对角线：

dp[i][j]=min(dp[i-1][j-1],min(sum1[i-1][j],sum2[i][j-1]))+1;

向左下方斜着的对角线：

dp[i][j]=min(dp[i-1][j+1],min(sum1[i-1][j],sum2[i][j+1]))+1;

第一个sum1记录从上到下最长的连续的0，sum2记录从左到右最长的连续的0

第二个sum1记录从上到下最长的连续的0，sum2记录从右到左最长的连续的0

dp[i][j]记录到i，j这个坐标能得到的最大正方形

最后取一个最大值就行了

看看代码

 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cstring>
 4 #include <algorithm>
 5 using namespace std;
 6 const int N=2505;
 7 int sum1[N][N],sum2[N][N],d[N][N],n,m,dp[N][N],ans;
 8 int main()
 9 {
10     scanf("%d %d",&n,&m);
11     for(int i=1;i<=n;i++)
12     {
13         for(int j=1;j<=m;j++)
14         {
15             scanf("%d",&d[i][j]);
16             if(!d[i][j])
17             {
18                 sum1[i][j]=sum1[i-1][j]+1;
19                 sum2[i][j]=sum2[i][j-1]+1;
20             }
21             else
22                 dp[i][j]=min(dp[i-1][j-1],min(sum1[i-1][j],sum2[i][j-1]))+1;
23             ans=max(ans,dp[i][j]);
24         }
25     }
26     memset(dp,0,sizeof(dp));
27     memset(sum1,0,sizeof(sum1));
28     memset(sum2,0,sizeof(sum2));
29     for(int i=1;i<=n;i++)
30         for(int j=m;j>=1;j--)
31         {
32             if(!d[i][j])
33             {
34                 sum1[i][j]=sum1[i-1][j]+1;
35                 sum2[i][j]=sum2[i][j+1]+1;
36             }
37             else
38                 dp[i][j]=min(dp[i-1][j+1],min(sum1[i-1][j],sum2[i][j+1]))+1;
39             ans=max(ans,dp[i][j]);
40         }
41     printf("%d\n",ans);
42     return 0;
43 }

思路很清楚了

转载于:https://www.cnblogs.com/wzrdl/p/9781752.html