线段AB上的点数和正方形CDEF上的点数哪个多？

答案是一样多！猜对了吗？猜是不够的，让我们建立一个一一对应关系

P(0.1357, 0.2468)--> P0.12345678 这样我们总能得到点的一一对应。同样线段和立方体的点数也是一样多！

这让我想起Z-value的多维到单维的映射方法。

同样的偶数个数和整数的个数是一样多的，不同长度的线段点数也一样多。实际上“在无穷大的世界里，部分可能等于全部”

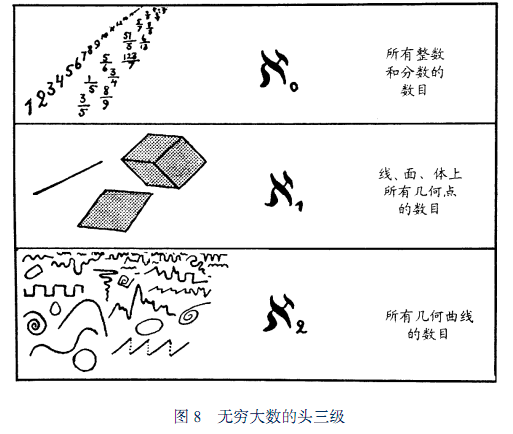
目前我们已经找到有三种无穷大级数aflai0<aflai1<aflai2, ，“各种曲线，包括任何一种奇形怪状的样式在内，它们的样式的数目比所有几何点的数目还要大。因此，应该把它看作是第三级无穷数列”。除此外，没有找到aflai3：

读《从一到无穷大》[美]加莫夫