PAM聚类算法详解-优快云博客

2019独角兽企业重金招聘Python工程师标准>>>

a、因为 K 均值聚类方法是基于均值的，所以它对异常值是敏感的，一个更稳健的方法是围绕在中心点的划分（PAM）。与其用质心（变量均值向量）表示类，不如用一个最有代表性的观测值来表示（称为中心点）。

b、K 均值聚类一般使用欧几里得距离，而 PAM 可以使用任意的距离来计算。因此， PAM可以容纳混合数据类型，并且不仅限于连续变量

PAM算法如下

a、随机选择 K 个观测值（每个都称为中心点）

b、计算观测值到各个中心点的距离/相异性

c、把每个观测值分配到最近的中心点

d、计算每个中心点到每个观测值的距离的总和（总成本）

e、选择一个该类中不是中心的点，并和中心点互换

f、重新把每个点分配到距它最近的中心点

g、再次计算总成本

h、如果总成本比步骤(4)计算总成本少，把新点作为中心点

i、重复步骤(5)~(6)直到中心点不再改变

使用 cluster 包中的 pam() 函数很实用基于中心点的划分方法，格式如下

pam(x , k, metric ="euclidean",stand = FLASE)

x：表示数据矩阵或数据框

k：表示聚类的个数

metric：表示使用的相似性/相异性的度量

stand：是一个逻辑值，表示是否有变量应该在计算该指标之前被标准化

对葡萄酒数据使用基于质心的划分方法

> library(cluster)
> set.seed(1234)
> fit.pam <- pam(wine[-1],3,stand=T) #基于中心点划分
> fit.pam$medoids #输出中心点
     Alcohol Malic  Ash Alcalinity Magnesium Phenols Flavanoids Nonflavanoids
[1,]   13.48  1.81 2.41       20.5       100    2.70       2.98          0.26
[2,]   12.25  1.73 2.12       19.0        80    1.65       2.03          0.37
[3,]   13.40  3.91 2.48       23.0       102    1.80       0.75          0.43
     Proanthocyanins Color  Hue Dilution Proline
[1,]            1.86   5.1 1.04     3.47     920
[2,]            1.63   3.4 1.00     3.17     510
[3,]            1.41   7.3 0.70     1.56     750
> library(cluster)
> set.seed(1234) #生成随机的种子，种子是为了让结果具有可重复性
> fit.pam <- pam(wine[-1],3,stand=T)
> fit.pam$medoids
     Alcohol Malic  Ash Alcalinity Magnesium Phenols Flavanoids Nonflavanoids
[1,]   13.48  1.81 2.41       20.5       100    2.70       2.98          0.26
[2,]   12.25  1.73 2.12       19.0        80    1.65       2.03          0.37
[3,]   13.40  3.91 2.48       23.0       102    1.80       0.75          0.43
     Proanthocyanins Color  Hue Dilution Proline
[1,]            1.86   5.1 1.04     3.47     920
[2,]            1.63   3.4 1.00     3.17     510
[3,]            1.41   7.3 0.70     1.56     750
> clusplot(fit.pam,main="Bivariate Cluster Plot") #画出聚类的方案，如下图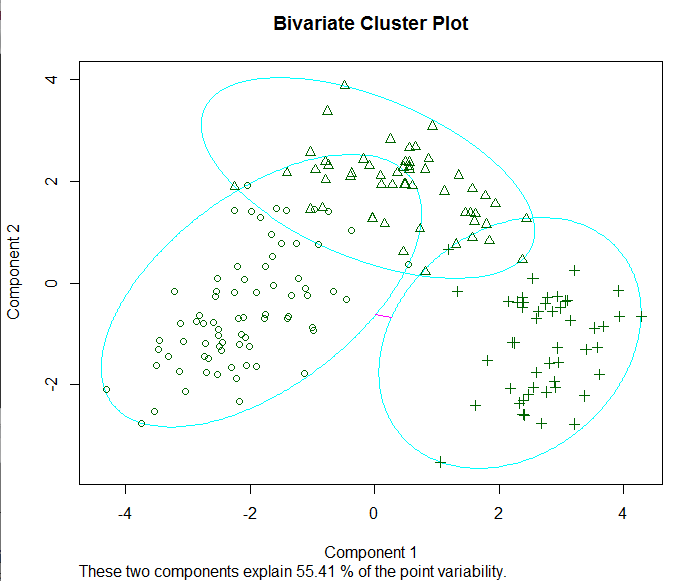

注意，这里得到的中心点是葡萄酒数据集中实际的观测值，在这种情况下，分别选择36、107和175观测值来代表三类。通过从13个测定变量上得到的前两个主成分绘制每一个观测的坐标来创建二元图。每个类用包含其所有点的最小面积椭圆表示。

还需要注意的是，PAM在这案例中的表现不如 K均值

> ct.pam <- table(wine$Type,fit.pam$clustering)
> ct.pam
   
     1  2  3
  1 59  0  0
  2 16 53  2
  3  0  1 47
> library(flexclust)
> randIndex(ct.pam)
      ARI 
0.6994957    #由0.9下降到0，7

转载于:https://my.oschina.net/u/1785519/blog/1564392