70. Climbing Stairs

最新推荐文章于 2024-01-18 13:59:59 发布

weixin_34239169

最新推荐文章于 2024-01-18 13:59:59 发布

阅读量48

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/skillking/p/9686501.html

本文探讨了经典的爬楼梯问题，提供了递归与动态规划两种解决方案。递归方法直观但效率低下，而动态规划通过避免重复计算显著提高了效率。

一、题目

　　1、审题

　　2、分析

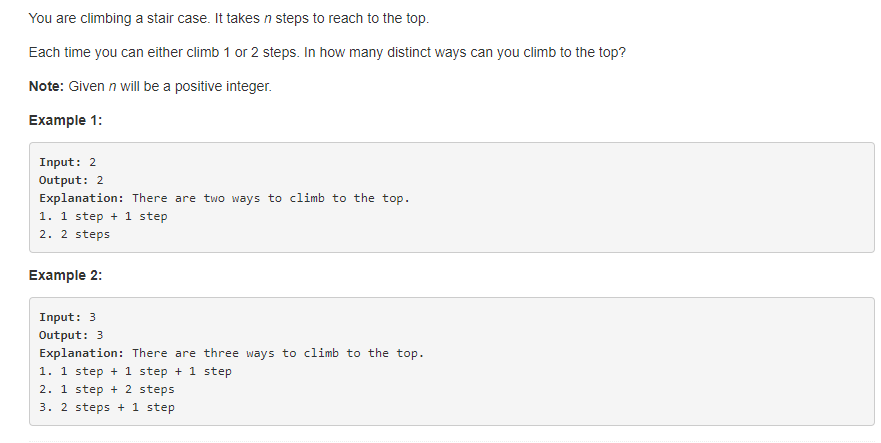
　　　　一次可以跳一步或者2步，求跳到 n 时共有几种跳法。

二、解答

　　1、思路：

　　　　方法一、

　　　　　　采用递归，到 n 级台阶记为 f（n）, 则到达 n 级台阶的跳法组成为： f(n) = f(n-1) + f(n-2) ；

　　　　　　注意：递归算法有许多重复的计算，导致时间超出了。。。。。。。

public int climbStairs(int n) {
        
        if(n == 1)
            return 1;
        if(n == 2)
            return 2;
        
        return climbStairs(n - 1) + climbStairs(n - 2);
    }

　　　　方法二、

　　　　　　将递归改为递推式。

　　　　　　从前往后推，利用前面用到的计算结果。

　　　　　　初始化时 dp[0] = dp[1] = 1, 利用 dp[n] = dp[n-1] + dp[n-2] 即可。

// 递推
    public int climbStairs2(int n) {
        
        if(n < 2)
            return 1;
        
        int[] dp = new int[3];
        dp[0] = 1;
        dp[1] = 1;
        
        for(int i = 2; i <= n; i++) {
            dp[2] = dp[0] + dp[1]; 
            dp[0] = dp[1];
            dp[1] = dp[2];
        }
        
        return dp[2];
    }