有关几何体中的最值

前言

典例剖析

例1【2019届高三理科数学第三轮模拟训练题】已知某圆台如图所示，它的上、下底面的直径分别为\(2\)和\(4\)，母线长为\(2\)，\(A\)为一母线的中点，\(B\)为过点\(A\)的轴截面截得的另一条母线与底面的交点，则在圆台侧面上从点\(A\)到点\(B\)的最短距离为【】

$A.4$ $B.5$ $C.6$ $D.7$

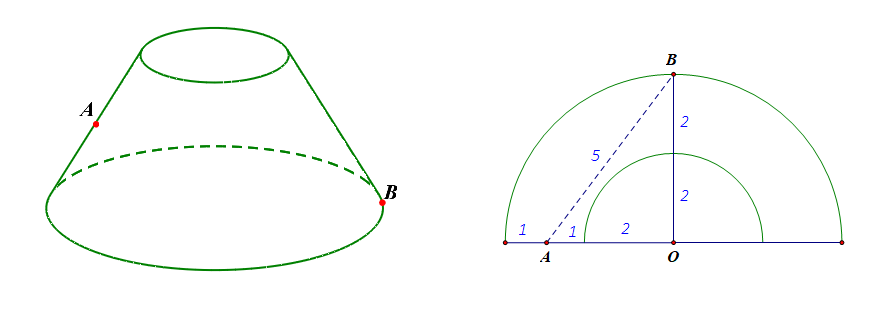
分析：由于上底面半径为\(1\)，上底面的周长为\(2\pi\)，又由题可知上底面对应圆锥的母线长也为\(2\)，故圆锥展开图为半圆，

将此圆台沿着过点\(A\)和\(B\)的轴截面切开，得到如右图所示的平面图，由平面内两点间的距离中线段最短可知，从点\(A\)到点\(B\)的最短距离即线段\(AB\)的长；

连结\(AB\)，则在\(\triangle AOB\)中，\(OA=3\)，\(OB=4\)，则\(AB=5\)，故选\(B\)。

例2【2019届高三理科数学第三轮模拟训练题】有一个长方体木块，三个侧面积分别为\(8\)，\(12\)，\(24\)，现将其削成一个正四面体模型，则该正四面体模型棱长的最大值为【】

$A.2$ $B.2\sqrt{2}$ $C.4$ $D.4\sqrt{2}$

分析：设长方体的长宽高分别为\(x\)，\(y\)，\(z\)，则由题可知有\(\left\{\begin{array}{l}{xy=8①}\\{yz=12②}\\{xz=24③}\end{array}\right.\)，三式相乘得到\(x^2y^2z^2=48^2④\)，

用④式分别除以①②③式，得到\(x=4\)，\(y=2\)，\(z=6\)，要想削成一个正四面体，

需要先取其最小棱的长度作为基础，首先得到棱长为\(2\)的正方体，然后由正方体切削成正四面体，

此时正四面体的棱长为该正方体的面对角线，故正四面体的棱长的最大值为\(2\sqrt{2}\)。

例3【2019届高三理科数学第三轮模拟训练题】一个棱锥的三视图如图，则该棱锥的最长棱的长度是【】

$A.2\sqrt{2}$ $B.3$ $C.4$ $D.\sqrt{7}$

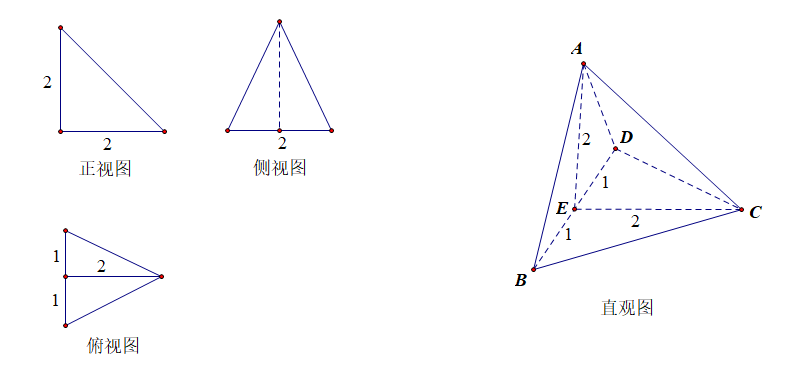
分析：做出其直观图，如右图所示，则最长棱为\(AC=2\sqrt{2}\)，故选\(A\).

转载于:https://www.cnblogs.com/wanghai0666/p/10978911.html