原帖地址:http://ogldev.atspace.co.uk/www/tutorial07/tutorial07.html
本章我们来学习一下,物体的旋转。所谓旋转,就是一个点,绕某个固定的轴转动一定的角度。在笛卡尔坐标系中,我们绕某个主轴转动时候,会保持该轴决定的分量不变,比如绕z轴旋转,z坐标分量不变,x,y分量变化,所以又称绕xy平面旋转,当然,我们也可以绕任意向量进行旋转操作。
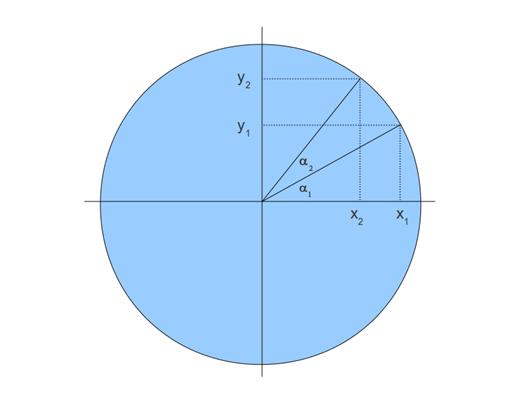
我们通过下面的图来了解一下旋转矩阵是如何产生的?
沿着圆把顶点从位置(x1,y1)移动到(x2,y2),由图可知,旋转的角度是 a2 ,假定圆是以弧度为单位,则有下面的式子:
x1=cos(a1)
y1=sin(a1)
x2=cos(a1+a2)
y2=sin(a1+a2)
用正弦和余弦公式展开,则有:
cos(a+b) = cosacosb - sinasinb
sin(a+b) = sinacosb+cosasinb
x2=cos(a1+a2) = cosa1cosa2 - sina1sina2 = x1cosa2 - y1sina2
y2=sin(a1+a2) = sina1cosa2 + cosa1sina2 = y1cosa2 + x1sina2
上面的式子是绕xy平面的旋转变化,转化到齐次坐标,则有下面的公式:
同理,绕y轴的旋转矩阵如下:
绕x轴旋转矩阵如下:
主要变化代码:
程序代码做很小的变动,就是改变世界矩阵的值,改用绕z轴渲染的矩阵。
World.m[0][0]=cosf(Scale); World.m[0][1]=-sinf(Scale); World.m[0][2]=0.0f; World.m[0][3]=0.0f;
World.m[1][0]=sinf(Scale); World.m[1][1]=cosf(Scale); World.m[1][2]=0.0f; World.m[1][3]=0.0f;
World.m[2][0]=0.0f; World.m[2][1]=0.0f; World.m[2][2]=1.0f; World.m[2][3]=0.0f;
World.m[3][0]=0.0f; World.m[3][1]=0.0f; World.m[3][2]=0.0f; World.m[3][3]=1.0f;
程序执行后界面如下:







 本篇博客详细解析了物体旋转的概念、数学表达及在编程中的应用,通过旋转矩阵的推导,展示了如何实现绕不同轴的二维旋转,并提供了实际代码示例,帮助读者掌握旋转操作的核心逻辑。
本篇博客详细解析了物体旋转的概念、数学表达及在编程中的应用,通过旋转矩阵的推导,展示了如何实现绕不同轴的二维旋转,并提供了实际代码示例,帮助读者掌握旋转操作的核心逻辑。
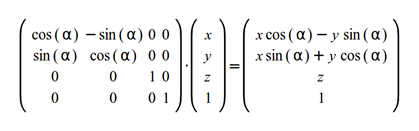
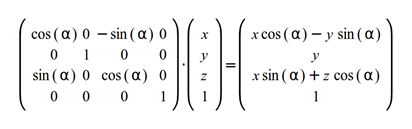
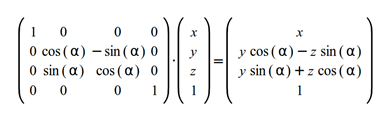


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








