RMQ问题的ST表实现-优快云博客

本文介绍了解决RMQ问题的一种高效算法——ST表。RMQ问题要求在给定区间内快速查找最大值或最小值。ST表通过预处理建立倍增区间，使用状态转移方程加速查询过程。文章详细解释了ST表的预处理步骤和查询方法，并提供了完整的代码示例。

【模板】RMQ问题的ST表实现

RMQ

本文主要讲解一下ST

定义：f[i][j]

预处理：f(i,0)=a_i

状态转移：将[i,j]

两段的长度均为2^j−1

得到f[i][j]=max(f[i][j−1],f[i+2^j⁻¹][j−1])

void RMQ(int N){
    /*注意外部循环从j开始，
    因为初始状态为f[i][0],
    以i为外层会有一些状态遍历不到。*/ 
    for(int j=1;j<=20;j++)  
        for(int i=1;i<=N;i++)
            if(i+(1<<j)-1<=N)
                f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}

查询：若需要查询的区间为[i,j]

这两个区间可以重复，因为两个区间是否相交对区间最值没有影响。（如下图）

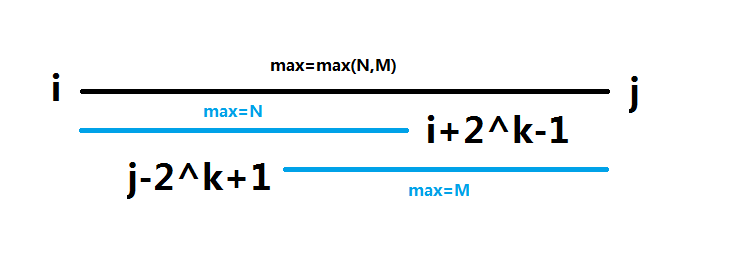
当然求区间和就肯定不行了。这也就是RMQ

因为区间的长度为j−i+1

则RMQ(A,i,j)=max{f(i,k),f(j−2^k+1,k)}

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
int a[100001],f[100001][20];
inline int read(){
    int x=0,f=1;
    char c=getchar();
    for(;!isdigit(c);c=getchar())
        if(c=='-')
            f=-1;
    for(;isdigit(c);c=getchar())
        x=x*10+c-'0';
    return x*f;
}
void RMQ(int N){
    for(int j=1;j<=20;j++)    
        for(int i=1;i<=N;i++)
            if(i+(1<<j)-1<=N)
                f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); 
}
int main(){
    int N=read(),M=read();
    for(int i=1;i<=N;i++) a[i]=read();
    for(int i=1;i<=N;i++) f[i][0]=a[i];
    RMQ(N); 
    while(M--){
        int i=read(),j=read();
         int k=(int)(log((double)(j-i+1))/log(2.0)); 
        printf("%d\n",max(f[i][k],f[j-(1<<k)+1][k]));
    }
    return 0;
}