一、表格与图形
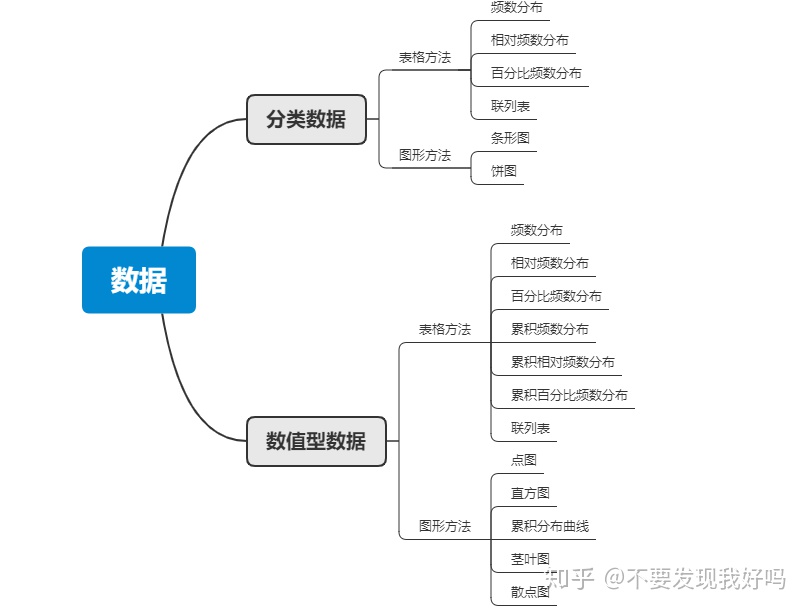
1.分类数据的汇总
①表格方法
频数分布：一种数据的表格形式汇总，表示在几个互不重叠组别中每一组所含观察值的数目（频数）。
相对频数：
百分比频数：
相对频数分布：表示每一组相对频数数据的表格汇总。
百分比频数分布：表示每一组百分比频数数据的表格汇总。
- 在任何一个频数分布中，频数的总和总是等于观察值的总和。
- 在任何一个相对频数分布中，相对频数的总和等于1.
- 在任何百分比频数分布中，百分比总和等于100.
联列表：对两个变量进行概括的一种表格方法。其中一个变量的分组情况用行表示，另一个变量的分组情况用列表式。
②图形方法
条形图
饼图
2.数值型数据汇总
①表格方法
频数分布：1)确定组数
2)确定组距：
3)确定组限
组中值：每组上限和下限的中间值。
相对频数分布
百分比频数分布
累计频数分布：显示不超过每组上限的观察值的数量。
累计相对频数分布：观察值小于或等于每组上限的个数占总数的比例。
累计百分比频数分布：观察值小于或等于每组上限的个数占总数的百分数。
联列表
②图形方法
点图：横轴表示观察值范围，每个观察值由位于坐标轴上方的点表示。
直方图
累积分布曲线
茎叶图
散点图
3.图形类别的选择
二、数值方法
1.
样本统计量：对样本进行概括的一些度量数值（如样本平均数
总体参数：对总体进行度量的一些度量数值（如总体平均数
点估计：用来估计相应总体参数的样本统计量（如
2.位置指标（位置度量）
①平均数/平均值：对数据的中心位置进行度量。计算方法是将所有数据值加总，再除以数据的个数。
数据是样本时，平均数用
数据是总体时，平均数用
样本平均数：
总体平均数：
②加权平均数：通过给每一个观察值分配一个反映其重要程度的权重而得到的一种平均数。
加权平均数：
③几何平均数：
几何平均数：
④中位数：对数据中心位置进行度量。计算方法是当数据按照升序排列时，处于数据中间位置的数据值（数据值为奇数时，为中间的数；为偶数时，为中间两数的平均值）。
当数据中含有异常值时，倾向使用中位数对数据中心趋势进行度量。
⑤众数：出现频率最高的数。
⑥百分位数：在一个数据集中，至少有
%的观察值大于或等于该值（第50个百分位数就是中位数）。
1）将数据按升序排列
2）计算位置指标
3）若
若
⑦四分位数：
3.变异指标
①极差：极差=最大值-最小值
②四分位距(IQR)：四分之三分位数与四分之一分位数之差，即中间50%数据旳极差。
四分位距=
③方差：平均离差平方和（离差：观察值与平均值的差）
总体方差：
样本方差：
方差越大，波动越大。
④标准差：方差的正平方根。
总体标准差：
样本标准差：
⑤变异系数：衡量标准差与平均数的相对大小
变异系数=
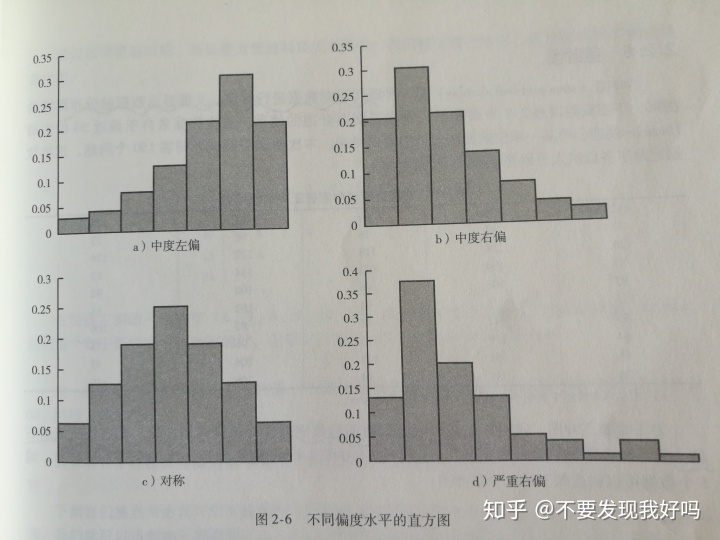
3.分布形态
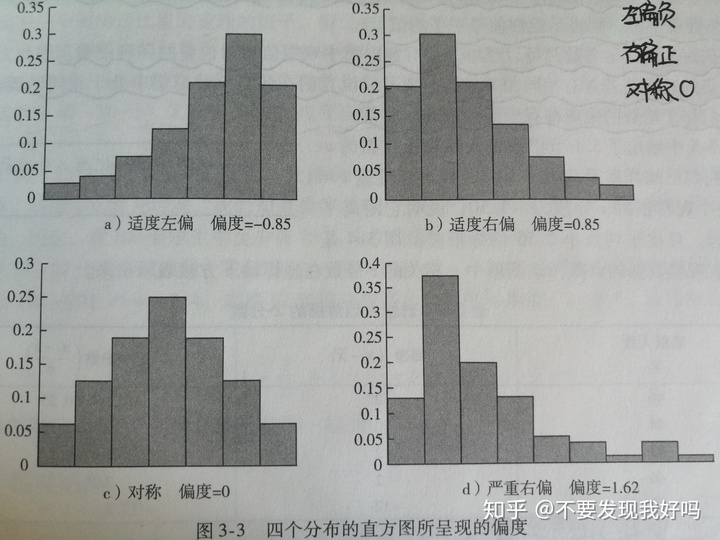
①偏度：数据分布形态的一种度量。
数据左偏，偏度为负值；数据右偏，偏度为正值；数据分布对称，偏度为0.
对于对称分布，平均数和中位数相等。数据右偏时，平均数>中位数；数据左偏时，平均数<中位数。
②z-分数/标准分数：
z-分数：
- 观察值>平均值时，z-分数>0;
- 观察值=平均值时，z-分数=0；
- 观察值<平均值时，z-分数<0.
③切比雪夫定理：与平均数的距离在
切比雪夫定理能使我们明确与平均数的距离在某个特定倍数的标准差之内的数据个数占全体数据的比例。适用于任何数据集。
④经验法则：确定与平均数的距离在某个特定倍数的标准差之内的数据项所占比例。
对于有钟型分布的数据：
- 大约有68%的数据项与平均数在1倍标准差之内
- 大约有95%的数据项与平均数在2倍标准差之内
- 几乎所有的数据项与平均数在3倍标准差之内
三、大量数据的数据集的特征展示
1.五数统计
使用以下五数对数据汇总：最小值、四分之一分位数、中位数、四分之三分位数、最大值。
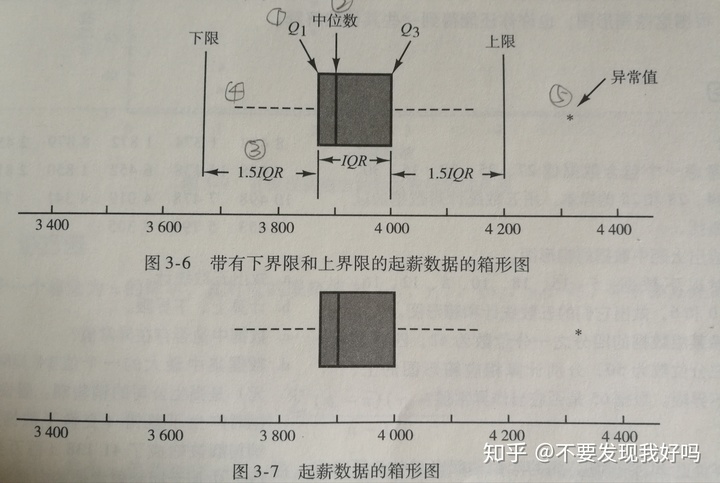
2.箱型图：根据五数统计对数据进行概括的图形方法。
绘制步骤：1）画一个箱体，边界为四分之一分位数和四分之三分位数。
2）在箱体内部中位数位置画一条垂线。
3）通过四分位距IQR=
4）绳索从箱体的边界一直画到3）计算出的界限以内的最大值和最小值处。
5）异常值用*标出。
3.两个变量间关系的度量
协方差：度量两个变量之间的线性强弱。越大于0，则正相关性越强，越小于0，则负相关性越强。
样本协方差：
总体协方差：
相关系数：取值在-1~1之间。越接近+1表示强的正线性关系，越接近-1表示强的负线性关系，接近0表示没有线性关系。
皮尔逊积矩相关系数：样本数据
总体数据
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
