这是我在知乎上的一个答案。个人非常喜欢这个证明。
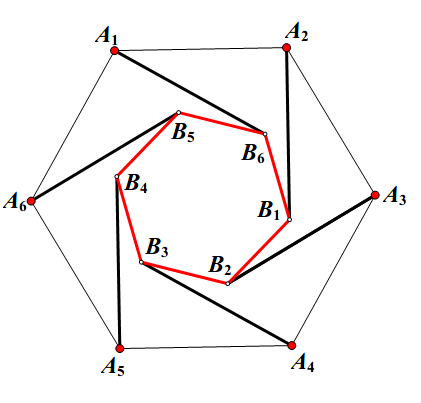
假如整点正六边形存在,一定有边长最小的一个,记作 .
.
以 为中心,将
为中心,将 逆时针旋转90度,得到
逆时针旋转90度,得到 。显然
。显然 也是整点。类似定义
也是整点。类似定义 ~
~ ,它们也都是整点。
,它们也都是整点。
如你所见,是一个更小的整点六边形,矛盾。
由此也可说明整点正三角形不存在。因为只要有整点正三角形,就一定有整点正六边形
值得注意的是,这样的证明是可以推广的(N>4时)。以下是五边形的情形。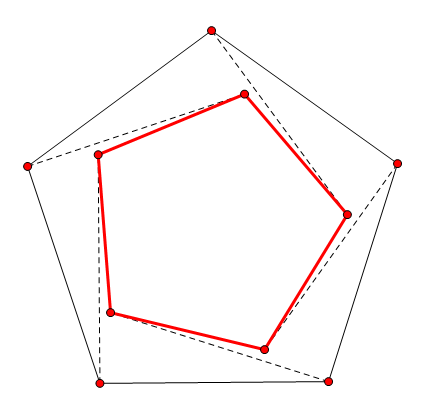
这是我在知乎上的一个答案。个人非常喜欢这个证明。

假如整点正六边形存在,一定有边长最小的一个,记作 .
.
以 为中心,将
为中心,将 逆时针旋转90度,得到
逆时针旋转90度,得到 。显然
。显然 也是整点。类似定义
也是整点。类似定义 ~
~ ,它们也都是整点。
,它们也都是整点。
如你所见,是一个更小的整点六边形,矛盾。
由此也可说明整点正三角形不存在。因为只要有整点正三角形,就一定有整点正六边形
值得注意的是,这样的证明是可以推广的(N>4时)。以下是五边形的情形。
转载于:https://www.cnblogs.com/dc93/p/4004613.html

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


