Generalized Linear Models 一般线性模型

最新推荐文章于 2022-04-21 07:12:08 发布

转载最新推荐文章于 2022-04-21 07:12:08 发布 · 145 阅读

·

0

·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/kyostone/p/5727529.html

文章标签：

#数据结构与算法

本文介绍了普通最小二乘法的基本原理及其数学推导过程，并探讨了在多重共线性情况下，如何通过岭回归解决估计不稳定的问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Ordinary Least Squares 普通最小二乘法

$\hat{y}(w, x) = w_0 + w_1 x_1 + ... + w_p x_p$

$\underset{w}{min\,} {|| X w - y||_2}^2$ 当达到最小值的时候，就达到最佳拟合直线

求关于系数w 最小二次方程的最小值，可以利用求对w偏导数

同上面等价的另外一种形式的表示：

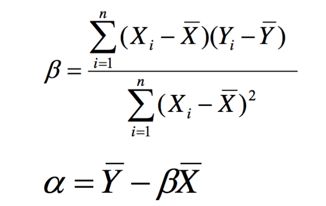
也可以简化成

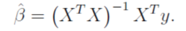
推导过程：

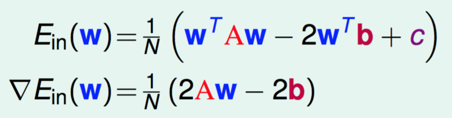
Ridge Regression 岭回归

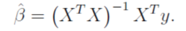
由于上式在多重共线性，会变成0，就会产生问题

通过变换成下面的式子，可以消除这个问题

k为岭参数，当k为0,得到最小二乘解，当岭参数趋向更大时,岭回归系数估计趋向于0

$\underset{w}{min\,} {{|| X w - y||_2}^2 + \alpha {||w||_2}^2}$

知识点：

多重共线性

回归模型中的变量存在高度相关性

有偏估计和无偏估计

个人理解（待修改）：由于直接计算比较困难，通过变换或加上辅助的因子来计算，变换后的计算是有偏估计

没有变换的计算是无偏估计

转载于:https://www.cnblogs.com/kyostone/p/5727529.html

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。