二叉查找树详解-优快云博客

2019独角兽企业重金招聘Python工程师标准>>>

三树

对于大量的输入数据，链表的线性访问时间太长，不宜使用。我们现在使用的数据结构叫做二叉查找数（binary search tree）。二叉查找数是两个流行库集合类map和set的实现基础。本章讨论的主题是：

了解树是如何用于实现几个流行的操作系统中的文件系统的。
了解树如何用来计算算术表达式的值。
指出如何利用树支持以Ο(logN)平均时间进行的各种搜索操作，以及如何细化以得到最坏情况时间界Ο(logN)。我们还讨论数据被存储在磁盘上时如何实现这些操作。
讨论并使用set和map类。

3.1 预备知识

数（tree）可以有几种方式定义。其中一种自然方式是递归的定义。一棵树是一些节点的集合。这个集合可以是空集;若不是空集，则树由称作跟（root）的节点r以及零个或者多个非空的（子）树T1、T2、…、Tk组成。这些子树中的每一颗的根都被来自跟r的一条有向的边（edge）所连接。每棵树的根叫做根r的儿子（child），而r是每棵树的根的父亲（parent）。图3-1显示了用递归定义的典型的树。

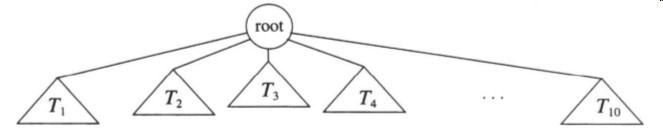
图3-1 一般的树

从递归定义中可以发现，一棵树是N个节点和N-1条边的集合。其中的一个节点叫作根。存在N-1条边的结论是由以下事实得出：每条边都将某个节点连接到它的父亲，而除去根节点外每一个节点都有一个父亲。

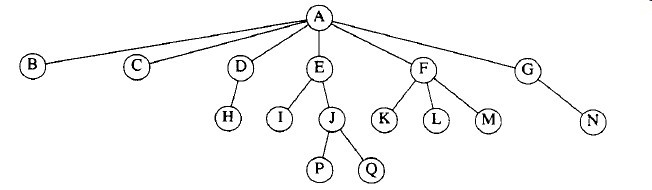
图3-2 一棵具体的树

节点A是根。没有儿子的节点称为叶（leaf）节点;具有相同父亲的节点称为兄弟（siblings）节点。

从节点n1到nk的路径（path）定义为节点n1，n2，…，nk的一个序列。使得对于1<=i<k，节点ni是ni+1的父亲。路径的长（length）为路径上的边的条数，即k-1。从每个节点到它自己有一条长为0的路径。注意，在一棵树中从根到每个节点恰好存在一条路径。

对任意节点n1，ni的深度（depth）为从根到ni的唯一路径的长。因此，根的深度为0，ni的高（height）是从ni到一片树叶的最长路径的长。

如果存在从n1到n2的一条路径，那么n1是n2的一位祖先（ancestor）而n2是n1的一个后裔（descendant）。如果n1≠n2，那么n1是n2的一位真祖先（proper ancestor）而n2是n1的一个真后裔（proper decendant）。

3.1.1 树的实现

实现树的一种方法是在每一个节点除数据外还要有一些链，来指向该节点的每一个儿子。下面是典型的节点声明：

struct TreeNode
{
  Object element;
  TreeNode *fileChild;
  TreeNode *nextSibling;
}

图3-3显示了一棵树如何用这种方法表示出来的。图中向下的箭头是指向firstChild的链。从左到右的箭头是指向nextSibling的链。

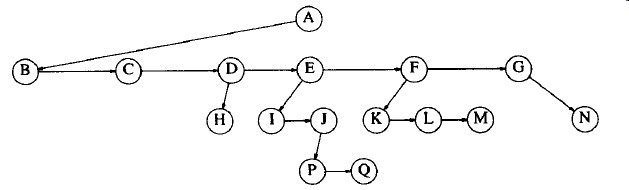
图3-3 在图3-2中所示的树的第一个儿子/下一个兄弟的表示法

3.1.2 树的遍历及应用

树有很多应用。流行的用法之一包括UNIX和DOS在内的许多常用操作系统的目录结构。图3-4是UNIX文件系统中的一个典型目录。

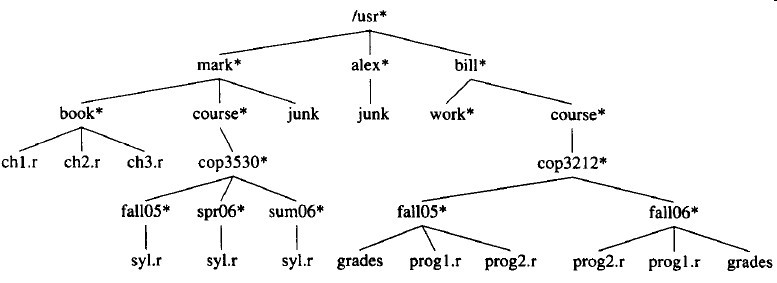
图3-4 UNIX目录

设想我们要列出目录中所有文件的名字。输出格式是：深度为di的文件将被di次跳格（tab）缩进后打印名。该算法的伪码如下：

void FileSystem::listAll( int depth = 0 ) const
{
  printName( depth ); //Print the name of object
  if( isDirectory() )
    for each file c in this directory( for each child )
      c.listAll( depth + 1 );
}

整个输入结果如图3-5。

图3-5 (前序)目录列表

这个遍历策略称为前序遍历（preorder traversal）。前序遍历中，对节点的处理工作是在它的诸儿子节点被处理之前进行的。如果有N个文件名需要输出，则运行时间就是Ο(N)。

另一种遍历树的常用方法是后序遍历（postorder traversal）。在后序遍历中，在一个节点的工作是在它的诸儿子节点被计算后进行的。例如，图3-6中圆括号内的数代表每个文件占用的磁盘块的个数。

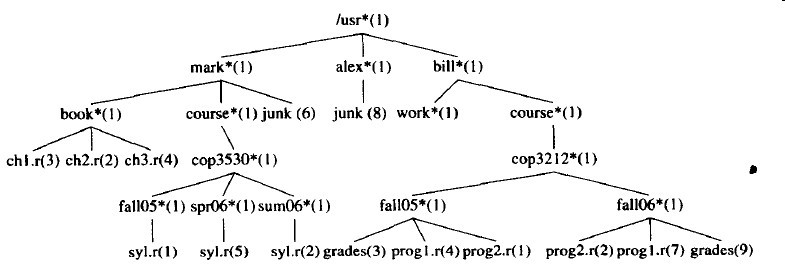
图3-6 经由后序遍历得到的带有文件大小的UNIX目录

下面是伪代码方法size实现了这种遍历策略：

int FileSystem::size( ) const
{
  int totalSize = sizeOfThisFile();
  
  if( isDirectory() )
    for each file c in this directory ( for each child )
      totalSize += c.size();
      
   return totalSize;
}

图3-7显示了每个目录或文件的大小如何由该算法产生的。

图3-7 函数size的跟踪

3.2 二叉树

二叉树（binary tree）是一棵每个节点都不能有多于两个儿子的树。

图3-8显示了一棵由一个根和两棵子树组成的二叉树，子树TL和TR均可能为空。

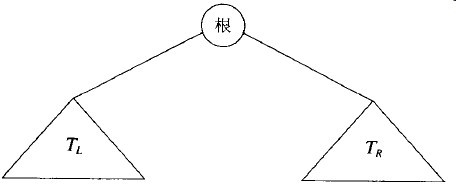
图3-8 一般二叉树

二叉树的一个性质是平均二叉树的深度要比节点个数N小得多。分析表明这个平均深度为Ο（√N），而对特殊类型的二叉树，即二叉查找树（binary search tree），其深度的平均值为Ο（logN）。遗憾的是，正如下图所示的例子，这个深度也可以大到N-1。

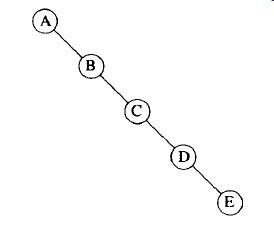
图3-9 最坏情况的二叉树

3.2.1 实现

在声明中，一个节点就是由element（元素）的信息加上两个到其他节点的引用（left和right）组成的结构。下面是二叉树节点的伪代码。

struct BinaryNode
{
  Object element; //The data in the node
  BinaryNode *left; //Left child
  BinaryNode *right; //Right child
}

3.2.2 一个例子——表达式树

图3-10是一个表达式树（expression tree）的例子。表达式树的树叶是操作数（operand），如常数或者变量名字，其他的节点为操作符（operator）。下面这个例子中，左子树的值是a+b*c，右子树的值是(d*e+f)*g。

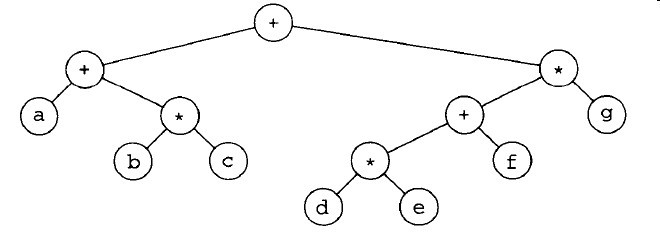
图3-10 (a+b*c)+((d*e+f)*g)

可以通过递归地产生一个带括号的左表达式，然后打印出在根处的操作符，最后再递归地产生一个带括号的右表达式而得到一个（对两个括号整体进行运算的）中缀表达式（infixexpression）。这种方法（左，节点，右）称为中序遍历（inorder traversal）。

另一个策略是递归地打印出左子树、右子树，然后打印操作符。如果应用这种策略于上面的树，则输出将是a b c * + d e * f + g * +。这一种是后序遍历（postorder traversal）。

还有一种遍历策略是先打印出操作符，然后递归地打印出左子树和右子树。其结果是：++a*bc*+*defg，这是不太常用的前缀（prefix）记法，这种遍历策略称为前序遍历（preorder traversal）。

构造一棵表达式树

下面给出一种算法把后缀表达式转变成表达式树。我们一次一个符号地读入表达式，如果符号是操作数，那么就建立一个单节点树并将它推入栈中。如果符号是操作树，它的左、右儿子分别是T2和T1。然后将指向这棵树的指针压入栈中。

设输入为：

a b + c d e + * *

前两个符号是操作数，因此创建两棵单节点树并将指向它们的指针压入栈中。

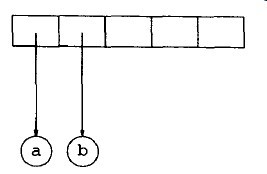
接着，“-”被读入，因此指向两棵数的指针被弹出，形成一棵新的树，并将指向它的指针压入栈中。

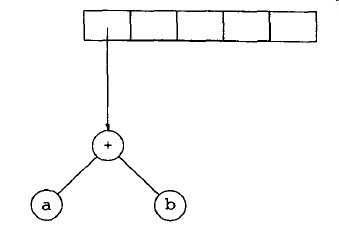
然后，c、d和e被读入，在每个单节点树创建后，指向对应的树的指针被压入栈中。

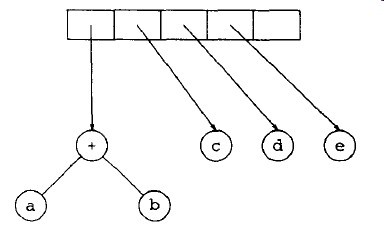
接下来读入“+”，因此两棵树合并。

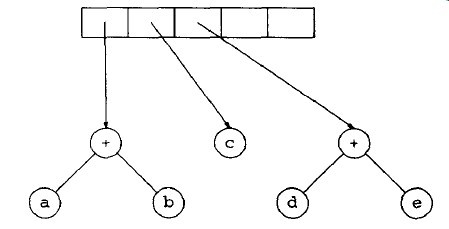
继续进行，读入“*”号，因此，弹出两棵树的指针并形成一棵新的树，“*”号是它的根。

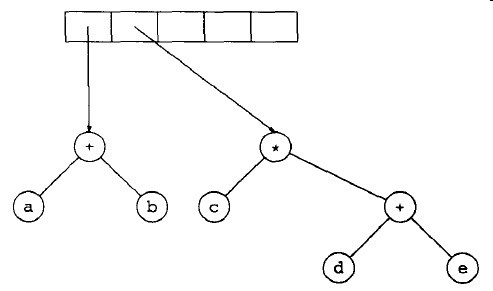
最后，读入最后一个符号，两棵树合并，而指向最后的树的指针被留在栈中。

3.3 查找树ADT——二叉查找树

二叉树的一个重要的应用是它们在查找中的应用。这里我们假设树中的每一个节点存储一项数据，都是互异的整数。

使二叉树称为二叉查找树的性质是，对于树中的每个节点X，它的左子树所有项的值小于X中的项，而它的右子树中的所有项的值大于X中的项。例如，在下图3-11中，左边的树是二叉查找树，但右边的树却不是。

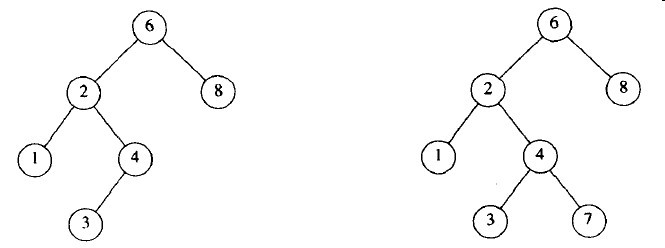
图3-11 两棵二叉树（只有左边的树是查找树）

下面给出二叉树的操作简要描述。由于树的递归定义，通常是递归地编写这些操作的例程。因为二叉查找树的平均深度是Ο（logN），所以不必担心栈空间被用完。下面是 BinarySearchTree类模板的接口(框架)。

template<typename Comparable>
class BinarySearchTree
{
  public:
    BinarySearchTree();
    BinarySearchTree( const BinarySearchTree & rhs );
    ~BinarySearchTree();
    
    const Comparable & findMin() const;
    const Comparable & findMax() const;
    bool contain( const Comparable & x ) const;
    bool isEmpty() const;
    void printTree() const;
    
    void makeEmpty();
    void insert( const Comparable & x );
    void remove( const Comparable & x );
    
    const BinarySearchTree & operator= ( const BinarySearchTree & rhs );
    
  private:
    struct BinaryNode
    {
      Comparable element;
      BinaryNode *left;
      BinaryNode *right;
      
      BinaryNode( const Comparable & theElement, BinaryNode *lt, BinaryNode *rt )
        : element( theElement ), left( lt ), right( rt )
    };
    
     BinaryNode *root;
     
     void insert( const Comparable & x, BinaryNode * & t  ) const;
     void remove( const Comparable & x, BinaryNode * & t  ) const;
     BinaryNode * findMin( BinaryNode *t ) const;
     BinaryNode * findMax( BinaryNode *t ) const;
     bool contains( const Comparable & x, BinaryNode *t ) const;
     void makeEmpty( BinaryNode * & t );
     void printTree( BinaryNode *t ) const;
     BinaryNode * clone( BinaryNode *t ) const; 
}

3.3.1 contains

如果在树T中有项为X的节点，那么contains就返回true，否则，若没有这样的节点，就返回false。若树为空就返回false。下面是公有成员函数调用私有递归成员函数的示例，

/**
 * Returns true if x is found in the tree
 */
 bool contains( const Comparable & x ) const
 {
   return contains( x, root );
 }
 
 /**
 * Returns true if x is found in the tree
 */
 void insert( const Comparable & * )
 {
   insert( x, root );
 }
 
 /**
 * Remove x from the tree.Nothing is done if x is not found
 */
 void remove( const Comparable & x )
 {
   remove( x, root );
 }

下面是二叉查找树的contains递归操作。

 /**
 * Internal method to test if an item is in a subtree.
 * x is item to search for.
 * f is the node that roots the subtree.
 */
 bool contains( const Comparable & x, BinaryNode *t ) const
 {
   if( t==NULL )
     return false;
   else if( x < t->element )
     return contains( x, t->left );
   else if( t->element < x )
     return contains( x, t->right );
   else
     return true;  //Match
 }

3.3.2 findMin和findMax

这个方法分别返回指向树中包含最小元和最大元的节点的指针。为执行findMin，从根开始并只要有左儿子就向左进行，终止点就是最小元素。findMax方法除分支朝右儿子其余过程相同。下面是递归实现的findMin：

/**
 * Internal method to find the smallest item in a subtree t.
 * Return node containing the smallest item.
 */
 BinaryNode *findMin( BinaryNode *t ) const
 {
   if( t == NULL )
     return NULL;
   if( t->left == NULL )
     return t;
   return findMin( t->left );
 }

下面是对二叉查找树findMax的非递归实现。

/**
 * Internal method to find the largest item in a subtree t.
 * Return node containing the largest item.
 */
  BinaryNode *findMax( BinaryNode *t ) const
  {
    if( t != NULL )
      while( t -> right != NULL )
        t = t->right;
    return t;
  }

3.3.3 insert

进行插入操作的方法在概念上很简单。为了将X插入到树T中，可以像使用contains那样沿着树查找。如果找到X，则什么也不做（或做一些“更新”）。否则将X插入到遍历的路径上的最后一点上。如图3-12在插入5以前和以后的二叉树。

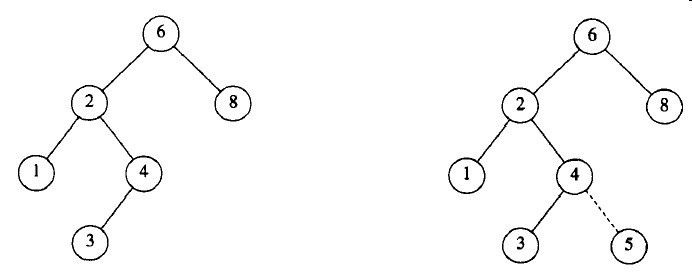
图3-12 在插入5以前和以后的二叉查找树

下面是插入方法的实现代码。

/**
 * Internal method to insert into a subtree.
 * x is the item to insert.
 * t is the node that roots the subtree.
 * Set the new root of the subtree.
 */
  void insert( const Comparable & x, BinaryNode * & t )
  {
    if( t ==NULL )
      t =new BinaryNode( x, NULL, NULL );
    else if( x < t->element )
      insert( x, t->left );
    else if( t->element < x )
      insert( x, t->right );
    else
      ; //Dupilicate; do nothing 
  }

3.3.4 remove

同许多数据结构一样，最困难的操作是删除。一旦发现要被删除的节点，就需要考虑几种可能的情况。如果一个节点是一片树叶，那么它可以被立即删除。如果节点有一个儿子，则该节点可以在其父节点调整它的链以绕过该节点后被删除（为了清楚起见，我们将明确画出链的指向），见图3-13。

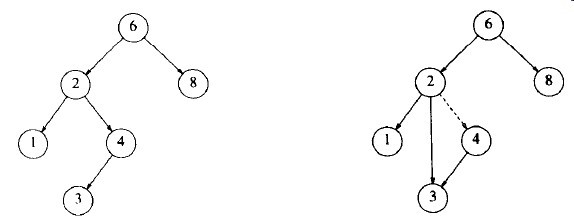
图3-13 具有一个儿子的节点4删除前后的情况

复杂的情况是处理具有两个儿子的节点。一般的删除策略是用其右子树的最小的数据（很容易找到）代替该节点的数据并递归地删除那个节点（现在它是空的）。因为右子树中的最小的节点不可能有左儿子，所以第二次remove就很容易。图3-14显示了一棵初始的树及其中一个节点被删除后的结果。

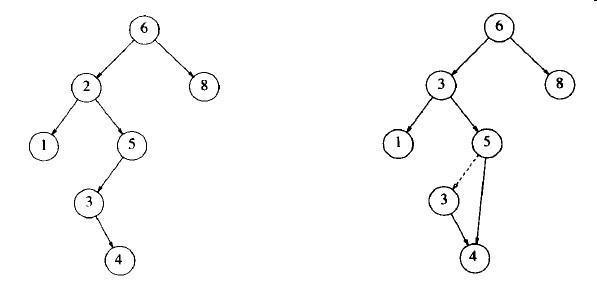
图3-14 删除有两个儿子的节点2前后情况

下面是一个删除的代码实现，但其效率不高，因为它沿该树进行两次搜索以查找和删除右子树中最小节点。通过编写一个特殊的removeMin方法可改善。

/**
 * Internal method to remove from a subtree.
 * x is the item to remove.
 * t is the node that roots the subtree.
 * Set the new root of the subtree.
 */
  void remove( const Comparable & x, BinaryNode * & t )
  {
    if( t == NULL )
      return; //Item not found;do nothing
    if( x < t->element )
      remove( x, t->left );
    else if( t->element < x )
      remove( x, t->right );
    else if( t->left != NULL && t->right != NULL ) //Two children
    {
      t->element = findMin( t->right )->element;
      remove( t->element, t->right );
    }
    else
    {
      BinaryNode *oldNode = t;
      t = ( t->left != NULL ) ? t->left : t->right;
      delete oldNode;
    }
  }

如果删除的次数不多，通常使用的策略是懒惰删除（lazy deletion）：当一个元素要被删除时，它仍然留在树中，而只是做了个被删除的记号。

3.3.5 析构函数和复制赋值操作符

与往常一样，析构函数调用makeEmpty。公有的makeEmpty则简单的调用私有的递归版的makeEmpty。下面是析构函数和递归makeEmpty成员函数。

/**
 * Destructor for the tree
 */
 ~BinarySearchTree()
 {
   makeEmpty();
 }
 /**
 * Internal method to make subtree empty.
 */
 void makeEmpty( BinaryNode * & t )
 {
   if( t != NULL )
   {
     makeEmpty( t->left );
     makeEmpty( t->right );
     delete t;
   }
   t = NULL;
 }

下面是operator和递归的clone成员函数。

 /**
 * Deep copy.
 */
 const BinarySearchTree & operator= ( const BinarySearchTree & rhs )
 {
   if( this != &rhs )
   {
     makeEmpty();
     root = clone( rhs.root );
   }
   return *this;
 }
 
 /**
 * Internal method to clone subtree .
 */
 BinaryNode * clone( BinaryNode *t ) const
 {
   if( t == NULL )
     return NULL;
     
   return new BinaryNode( t->element, clone( t->left ), clone( t->right ) );
 }