【leetcode】861. Score After Flipping Matrix-优快云博客

本文介绍了一种通过变换矩阵中的行和列来最大化其转换为二进制数后的总和的方法。关键在于确保每行最高位为1，并尽可能使每一列中1的数量多于0。该算法首先遍历所有行，将最高位设为1；然后遍历所有列，如果0的数量多于1，则反转该列。

题目如下：

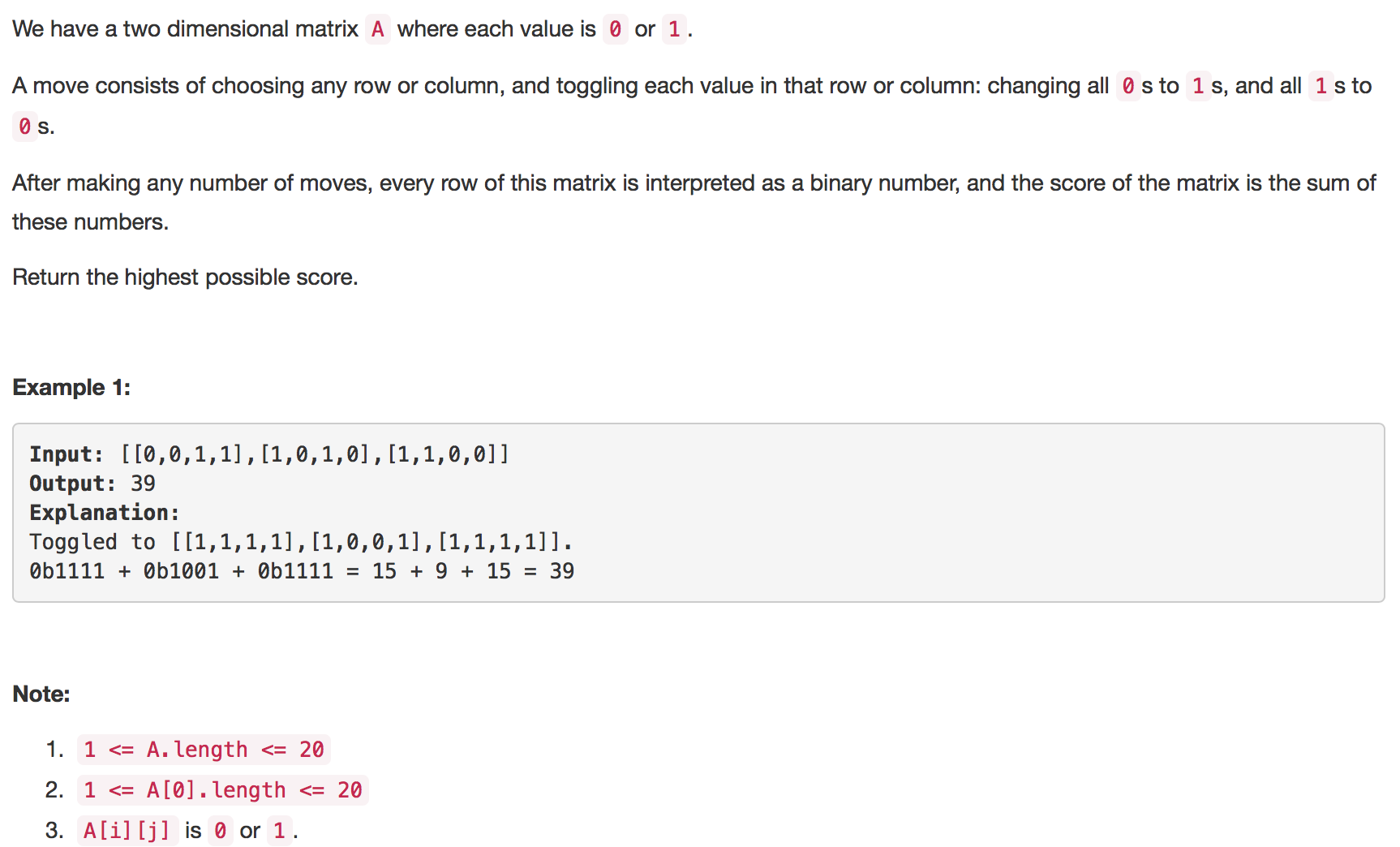
解题思路：本题需要知道一个数字规律，即pow(2,n) > sum(pow(2,0)+pow(2,1)+...+pow(2,n-1))。所以，为了获得最大值，要保证所有行的最高位是1，即需要优先进行行变换，把最高位变成1。接下来就是列变换，把0多于1的列做变换变成1多于0的列即可。

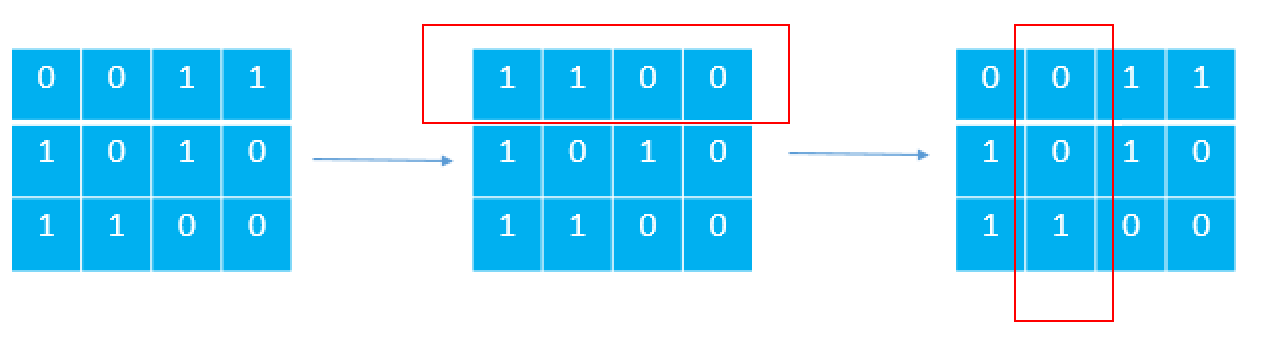代码如下：

class Solution(object):
    def matrixScore(self, A):
        """
        :type A: List[List[int]]
        :rtype: int
        """
        if len(A) == 0 or len(A[0]) == 0:
            return 0
        #set the highest bit to 1.Since pow(2,N) > sum(pow(2,0) + pow(2,1) + ...+pow(2,n-1)
        for i in range(len(A)):
            if A[i][0] == 1:
                continue
            else:
                for j in range(len(A[i])):
                    if A[i][j] == 0:
                        A[i][j] = 1
                    else:
                        A[i][j] = 0
        row = len(A)
        column = len(A[0])
        for i in range(column):
            count1 = 0
            count0 = 0
            for j in range(row):
                if A[j][i] == 0:
                    count0 += 1
                else:
                    count1 += 1
            if count0 > count1:
                #convert
                for j in range(row):
                    if A[j][i] == 0:
                        A[j][i] = 1
                    else:
                        A[j][i] = 0
        res = 0
        for i in A:
            v = ''.join([str(j) for j in i])
            res += int(v,2)
        return res