Xor Submatrix(Trie树)

最新推荐文章于 2025-02-18 21:43:37 发布

原创最新推荐文章于 2025-02-18 21:43:37 发布 · 231 阅读

0 ·

CC 4.0 BY-SA版权

CS Academy 专栏收录该内容

4 篇文章

订阅专栏

本文介绍了一种解决最大子矩阵异或和问题的方法。通过分析异或特性和使用Trie树来高效处理子矩阵的异或和计算，实现O(n*n*logn)的时间复杂度。

Xor Submatrix

Time limit: 2000 ms
Memory limit: 512 MB

Given an array $V$ of size $N$ and another array $U$ of size $M$ , we build a matrix $A$ of size $\times M$ , where $A_{i, j} = V_i\ \text{xor}\ U_j$ .

We say the score of a submatrix of $A$ is the xor sum of all its elements. Find the submatrix with the highest score.

Standard input

The first line contains two integers $N$ and $M$ .

The second line contains $N$ integers representing the elements of $V$ .

The thirst line contains $M$ integers representing the elements of $U$ .

Standard output

Print the highest possible score on the first line.

Constraints and notes

$\leq N, M \leq 1000$
$\leq V_i < 2^{29}$
$\leq U_i < 2^{29}$

Input	Output	Explanation
3 4 5 3 1 2 1 2 4	7
3 3 10 12 4 5 10 9	15
3 3 1 2 1 4 2 8	15

题意：给你两个序列V跟U，构造一个矩阵A，其中Aij = Ui ^ Vj

求最大的子矩阵的异或和。

思路：根据异或的特性，很容易想到跟奇偶有关，所以可以将子矩阵分成四种情况讨论：

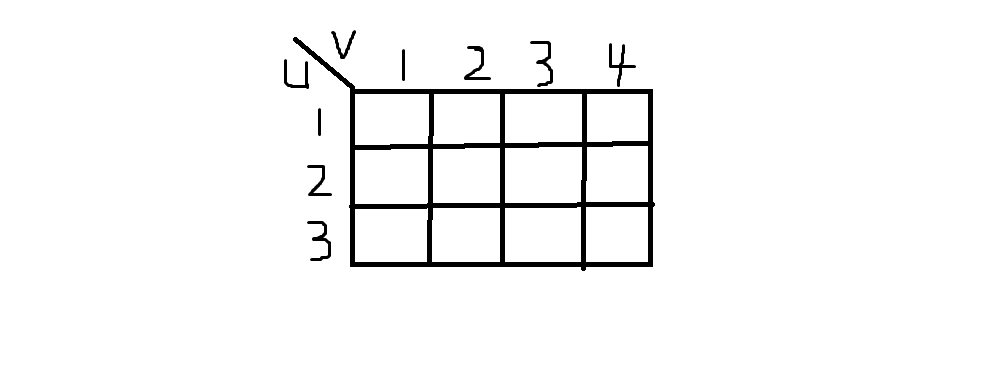
偶数 * 偶数：序列U跟V的每个数都被异或了偶数次，故结果恒为0.

偶数 * 奇数：序列V的每个数都被异或了偶数次，故只需计算计算序列U中长度为偶数的异或和情况。

奇数 * 偶数：序列U的每个数都被异或了偶数次，故只需计算计算序列V中长度为偶数的异或和情况。

奇数 * 奇数：序列U跟V中长度为奇数的所有情况的异或，这个不能暴力处理，可以先将U序列或者V

序列的长度为奇数的的异或和插入到Trie树中，再分析另一个序列中长度为奇数的异或

和与另一序列异或得到的最大值。相当于求：一个数与一个另一个序列的最大异或和。

时间复杂度为O(n * n * logn)

代码如下：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace	std;
const int maxn = 10000000;
struct Trie
{
	int next[maxn][2];
	int root;
	void init()
	{
		memset(next,-1,sizeof next);
		root = 0;
	}
	void insert(int x)
	{
		int now = 0;
		for(int i=31;i>=0;i--)
		{
			if(x&(1<<i))
			{
				if(next[now][1]>=0) now = next[now][1];
				else 
				{
					next[now][1] = ++root;
					now = next[now][1];
				}
			}
			else 
			{
				if(next[now][0]>0) now = next[now][0];
				else 
				{
					next[now][0] = ++root;
					now = next[now][0];
				}
			}
		}
	}

	int query(int x)
	{
		int res = 0,now = 0;
		for(int i=31;i>=0;i--)
		{
			int tmp = x&(1<<i);
			if(next[now][!tmp]>=0)
			{
				res |= (1<<i);
				now = next[now][!tmp];
			}
			else now = next[now][tmp];
		}
		return res;
	}
};
Trie ac;
int a[1010],b[1010];
int prea[1010],preb[1010];
int main()
{
	
	int n,m; scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) 
		scanf("%d",&a[i]),prea[i] = prea[i-1]^a[i];
	for(int i=1;i<=m;i++) 
		scanf("%d",&b[i]),preb[i] = preb[i-1]^b[i];
	int res = 0;
	for(int i=1;i<=n;i++)
		for(int j=2;i+j-1<=n;j+=2) res = max(res,prea[i+j-1]^prea[i-1]); 
	for(int i=1;i<=m;i++)
		for(int j=2;i+j-1<=m;j+=2) res = max(res,preb[i+j-1]^preb[i-1]);
	ac.init();
	for(int i=1;i<=n;i++)
		for(int j=1;i+j-1<=n;j+=2) ac.insert(prea[i+j-1]^prea[i-1]);
	for(int i=1;i<=m;i++)
		for(int j=1;i+j-1<=m;j+=2) res = max(res,ac.query(preb[i+j-1]^preb[i-1]));
	printf("%d\n",res);
}