HLG 1065 The Gougu Theorem【勾股数】

最新推荐文章于 2022-12-12 23:40:06 发布

weixin_34195364

最新推荐文章于 2022-12-12 23:40:06 发布

阅读量148

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/dream-wind/archive/2012/03/16/2400635.html

本文介绍勾股定理的历史及其在中国与西方的不同称谓，并探讨如何通过算法寻找特定条件下勾股数的正整数解。此外，还提供了一段C语言代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description

Pythagorean Theorem is "humanity's greatest scientific discoveries of the ten" is a basic elementary geometry theorems. "This theorem has a very long history, almost all ancient civilizations (Greece, China, Egypt, Babylon, India, etc.) have studied this theorem. Pythagorean Theorem in the West known as the Pythagorean Theorem, are said to Ancient Greek mathematician and philosopher Pythagoras (Pythagoras, BC572 ~ BC497) was first discovered in BC550.

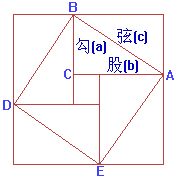
Pythagorean Theorem in China known as the Gougu/勾股Theorem. Around 1100 BC, the Western Zhou period, the ancient Chinese mathematician, Shanggao, first described the Gougu Theorem. In the famous ancient mathematics book, 《九章算术》,the proof was given (left). The Gougu Theorem is that "in the right triangle, the sum of the squares of two right sides is equal to the square of the hypotenuse." In other words, the three sides (a, b, c) of right-angled triangle satisfies the following equation:

a²+b²=c²

Where a is called勾/Gou, b is股/Gu, and c is弦/Xian.

For given c, how many different positive integer solutions are there? ((a,b,c）are relatively-prime. ) It is an interesting problem.

Now, your task is to solve it.

勾股数：

a=2*m*n;

b=m^2-n^2;

c=m^2+n^2;

code:

View Code

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<stdlib.h>
int cmp(const void*p1,const void*p2)
{
return *(int*)p1-*(int*)p2;
}
int huzhi(int x,int y)
{
int t;
while(x!=0)
 {
  t=y%x;
  y=x;
  x=t;
 }
if(y==1)
return 1;
return 0;
}
int main()
{
int b[50000],c[1000];
int n,i,q,k=0,m=0;
 memset(b,0,sizeof(b));
for(i=1;i*i<=(1<<15);i++)
 {
  b[i*i]=1;
 }
while(scanf("%d",&n),n)
 {
  k++;

  q=0;
for(i=(int)sqrt(n/2);i*i<=n;i++)
if(b[n-i*i]&&i*i-(n-i*i)>0&&huzhi(i*i-(n-i*i),2*i*(int)sqrt(n-i*i)))
     c[q++]=(i*i-(n-i*i)<2*i*(int)sqrt(n-i*i))?i*i-(n-i*i):2*i*(int)sqrt(n-i*i);
   qsort(c,q,sizeof(c[0]),cmp);
   printf("Case %d:\n",k);
   printf("There are %d solution(s).\n",q);
for(i=0;i<q;i++)
   printf("%d^2 + %d^2 = %d^2\n",c[i],(int)sqrt((n+c[i])*(n-c[i])),n);
   putchar('\n');
 }
return 0;
}