POJ 3243 Clever Y（babyStepGiantStep）-优快云博客

本文提供了一种解决POJ 3243问题的方法，该问题要求找到满足特定模幂等式的未知数x。文章详细介绍了如何通过预处理小范围内的可能解并使用扩展版Baby Step Giant Step算法来高效地解决此问题。

题意：给定A、B、P，求x满足A^x%P=B。

思路：首先，这里的(A,P)不一定等于1，即A与P不一定互质，不能直接利用babyStepGiantStep。下面我们进行变换。首先我们暴力x到100，若在100以内有解则直接返回。下面我们讨论的是x大于等于100的情况。



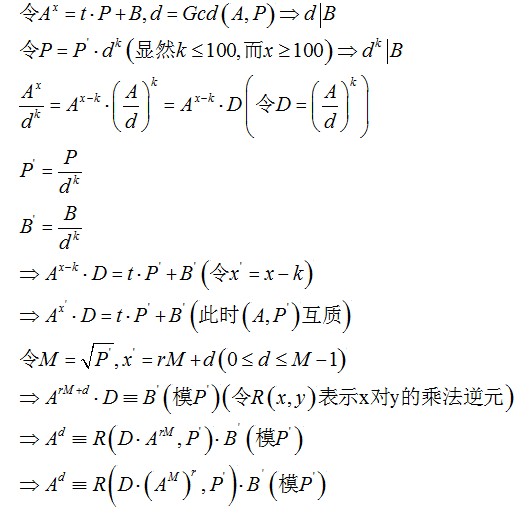
i64 P,A,B;

i64 power(i64 a,i64 b,i64 p)
{
    i64 ans=1;
    while(b)
    {
        if(b&1) ans=ans*a%p;
        a=a*a%p;
        b>>=1;
    }
    return ans;
}

struct node
{
    int id,k,next;
};


node edges[N];
int head[N],e;

void Add(int id,int k)
{
    int x=k%N,i;
    for(i=head[x];i!=-1;i=edges[i].next)
    {
        if(edges[i].k==k) return;
    }
    edges[e].id=id;
    edges[e].k=k;
    edges[e].next=head[x];
    head[x]=e++;
}


int find(int k)
{
    int x=k%N,i;
    for(i=head[x];i!=-1;i=edges[i].next)
    {
        if(edges[i].k==k) return edges[i].id;
    }
    return -1;
}




i64 Gcd(i64 x,i64 y)
{
    return !y?x:Gcd(y,x%y);
}

i64 exGcd(i64 a,i64 b,i64 &x,i64 &y)
{
    i64 t,d;
    if(!b)
    {
        x=1;
        y=0;
        return a;
    }
    d=exGcd(b,a%b,x,y);
    t=x;
    x=y;
    y=t-a/b*y;
    return d;
}


i64 reverse(i64 a,i64 b)
{
    i64 x,y;
    exGcd(a,b,x,y);
    return (x%b+b)%b;
}



i64 exBabyStepGiantStep(int A,int B,int P)
{
	clr(head,-1); e=0;
	i64 d=1,i;
	FOR0(i,100)
	{
	    if(d==B) return i;
	    d=d*A%P;
	}

	i64 D=1%P,k=0,temp;
    while((temp=Gcd(A,P))!=1)
    {
        if(B%temp) return -1;
        k++; P/=temp; B/=temp; D=D*A/temp%P;
    }
    i64 M=ceil(sqrt(1.0*P))+1;
    d=1;
    FOR0(i,M) Add(i,d),d=d*A%P;
    i64 K=power(A,M,P);
    FOR0(i,M)
    {
        temp=reverse(D,P)*B%P;
 		if((d=find(temp))!=-1) return i*M+d+k;
 		D=D*K%P;
 	}
 	return -1;
}

int main()
{
    Rush(A)
    {
        RD(P,B);
        if(A+B+P==0) break;
        i64 ans=exBabyStepGiantStep(A,B,P);
        if(ans<0) puts("No Solution");
        else PR(ans);
    }
    return 0;
}

转载于:https://www.cnblogs.com/jianglangcaijin/archive/2013/04/26/3046061.html