干粮 -- 计算机程序设计艺术(The Art of Computer Design) - 1

最新推荐文章于 2024-12-14 01:55:12 发布

转载最新推荐文章于 2024-12-14 01:55:12 发布 · 111 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/zhuisha/archive/2010/05/05/1727621.html

本文深入探讨了算法的基本概念，通过欧几里得算法为例详细解释了算法的五大特性，并进一步给出了算法的数学定义，帮助读者理解算法的本质。

CHAPTER ONE

1.1 算法

解决的问题:什么是算法.

举例:

算法E(欧几里得算法):给定两个正整数m和n,求他们的最大公因子.

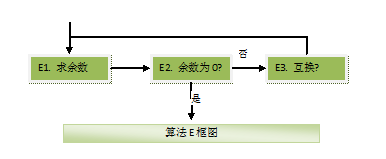
E 1. (求余数)以n除m并令r为所得余数(0≤r＜n).

E 2. (余数为0?)若r=0 算法结束;n即为答案.

E 3. (互换)令m←n, n←r,并返回步骤E1

框图如下:

算法的五个特性:

1) 有穷性一个算法必须总是在执行有穷步之后结束.算法E是满足该条件的.因为在步骤E1之后,r＜n,所以如果r≠0，下一次执行步骤E1时,n的值已经减小,正整数的递降序列一定会终止,因此对于任意的m和n,算法E肯定会在有穷次后结束.

2) 确定性算法的每一个步骤必须是确切定义的

3) 输入一个算法必须有0个或多个输入(E中有两个输入m和n)

4) 输出一个算法必须有一个或多个输出(E中最终输出的n)

5) 可行性一般来说,还期望一个算法是可行的.

算法的5个特性中,有穷性显然是不够的,因为一个算法不光要可以执行,而且要高效.

算法的数学定义:

借助数学的集合论思想,我们可以定义算法如下:一个计算方法是一个四字式(Q,I,Ω,f),其中q是一个包含I和Ω的集合,f是由Q到它自身的一个函数. f应当保留Ω的每个元素不动(me:注意Ω是输出集合.),也就是说,对于Ω中的所有元素q 必有f(q)=q. 这四个量Q,I, Ω,f 分别用来表示计算的状态,输入,输出和计算的规则. 集合I中的每个输入定义一个计算序列x₀, x₁, x₂... 如下:

x₀ = x 且 x_k+1 = f(x_k) 对于任意的 k≥0 (1)

如果有k是使得x_k在Ω中的最小整数(此处的最小是k最小,而不是x_k),则称计算序列在第k步终止. 这种情况下也说:x产生输出x_k(注意,如果x_k在Ω中,则x_k+1也是,因为在这样的情况下, x_k+1=x_k(me:对于输出集合欧姆f将其中的任意元素q映射到自身q,即f(q)=q)).某些计算序列可能永不终止,而一个算法是对于I中的所有元素x,都在有穷多的步骤内终止的一个计算方法.

(me:一个算法是一个有穷的计算方法.而一个计算方法是一(Q,I,Ω,f)的四元组)

例子:算法E,设Q为所有的单个数 (n) 所有的有序偶 (m,n) 和所有有序的四字式(四元组)(m,n,r,1),(m,n,r,2)以及(m,n,p,3)的集合,其中m,n和p为正整数,而r是一个非负整数.设I是所有有序偶(m,n)做成的子集,并设Ω是所有单个的数(n)的子集.设f定义如下:

f(m,n) = (m,n,0,1); f(n) = n;

f(m,n,r,1) = (m,n,m%n,2);

f(m,n,r,2) = (n) 如果r=0, 否则(m,n,r,3).

f(m,n,p,3) = (n,p,p,1)

这个更数学的方式表达的意思跟算法E 的各个步骤之间的对应关系式显然的.

转载于:https://www.cnblogs.com/zhuisha/archive/2010/05/05/1727621.html