陶哲轩实分析 命题 7.3.4 (Cauchy 准则) 证明

设$(a_n)_{n=1}^{\infty}$是一个非负实数的不增序列，那么级数$\sum_{n=1}^{\infty}a_n$收敛当且仅当级数
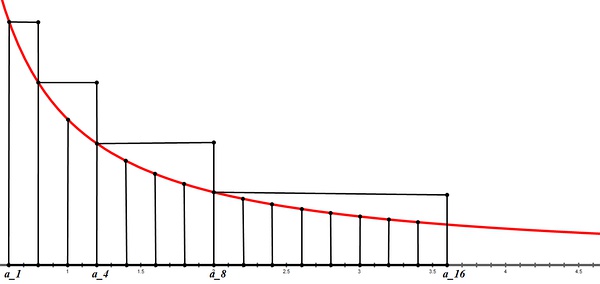
$$\sum_{k=0}^{\infty}2^ka_{2^k}=a_1+2a_2+4a_4+8a_8+\cdots$$收敛.

 

证明：$\Leftarrow$:当$\sum_{k=0}^{\infty}2^ka_{2^k}$收敛时.根据数学归纳法易得$\forall N\in\mathbb{N},\sum_{k=0}^{N}2^ka_{2^k}\geq \sum_{k=0}^{2^N}a_k$.所以$\sum_{k=1}^{\infty}a_n$收敛.

$\Rightarrow$:当$\sum_{n=1}^{\infty}a_n$收敛时，说明对于任意给定的正实数$\varepsilon$,都存在相应的整数$N$,使得$|\sum_{n=N}^{\infty}a_n|\leq\varepsilon$.所以很容易推得$\sum_{k=0}^{\infty}2^ka_{2^k}$收敛.

 

 

 

 

转载于:https://www.cnblogs.com/yeluqing/archive/2012/11/02/3828206.html