leetcode 120 triangle

最新推荐文章于 2025-09-03 19:44:06 发布

转载最新推荐文章于 2025-09-03 19:44:06 发布 · 70 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/legendcong/p/9139992.html

文章标签：

#数据结构与算法

本文介绍了求解三角形网格中从顶点到底边的最小路径和问题的两种方法：递归深度优先搜索（DFS）及自底向上的动态规划。通过分析递归方法存在的问题，进而提出更优的动态规划解决方案。

#include <cstdio>
#include <vector>
using namespace std;
class Solution {
private:
     void DFS(int index,int y,int ans,int n,int &min, vector<vector<int>> triangle)//n是层数,index是序号，max是最大值
    {
        if (index == n )
        {
            if (ans < min)
            {
                min = ans;
            }
            return;
        }
            DFS(index + 1,y, ans + triangle[index][y],n,min, triangle);
         if(index!=0)
            DFS(index + 1, y+1, ans + triangle[index][y+1], n, min, triangle);
    }
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int min = 1e9;
        DFS(0,0,0,triangle.size(),min,triangle);
        return min;
    }
};

1.递归写法妥妥的超时,反复DFS。

2.正确的操作，自底向上的进行动态规划，根据题目特点找出这个triangle的元素编号规律，发现只要写成和的形式的数就可以了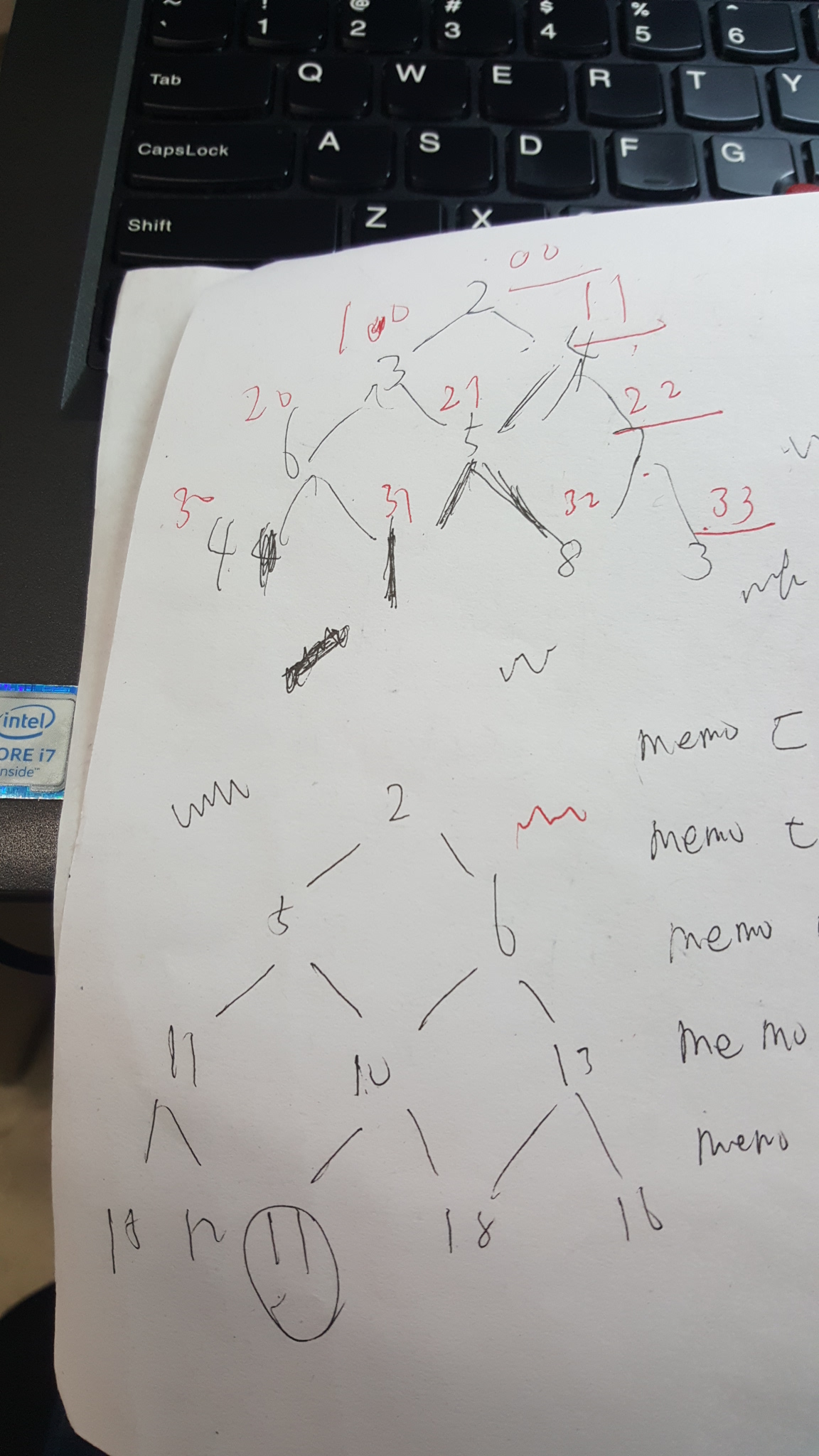

3.然后进行memo数组的建立，遍历最底层的元素，找出其中的最小值即可完成。

#include <bits/stdc++.h>
using namespace std;
class Solution {
    private:
    int min(int a, int b)
    {
        return a < b ? a : b;
    }
public:
    int minimumTotal(vector<vector<int>>& triangle) {
      // vector<vector<int>>memo;
        int n = triangle.size();
        vector<vector<int> > memo(n, vector<int>(n, 0));//二维数组初始化.
        int index = 0;
        int x, y;
        memo[0][0] = triangle[0][0];
        for (index = 1; index < n; index++)
        {
            for (y = 0; y < index + 1; y++)
            {
                if (y == 0)
                {
                    memo[index][y] = triangle[index][y] + memo[index - 1][0];
                }
                else if (y == index)
                {
                    memo[index][y] = triangle[index][y] + memo[index - 1][y - 1];
                }
                else
                {
                    memo[index][y] = triangle[index][y] + min(memo[index - 1][y - 1], memo[index - 1][y]);
                }
            }
        }
        int min = 1e9;
        for (int i = 0; i <= n - 1; i++)
        {
            if (memo[n - 1][i] < min)
            {
                min = memo[n - 1][i];
            }
        }
        return min;
    }
};