剑指Offer——面试题26：复杂链表的复制-优快云博客

本文介绍了一种包含m_pNext及m_pSibling指针的复杂链表复制方法。提供了两种思路，一是就地复制并解开链表，二是利用哈希表进行节点地址映射。附带测试代码验证算法正确性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：请实现函数ComplexListNode* Clone(ComplexListNode* pHead),复制一个复杂链表。在复杂链表中，每个节点除了有一个m_pNext指针指向下一个节点外，还有一个m_pSibling指向链表中的任意节点或者NULL。节点的定义如下。

typedef struct ComplexListNode_
{
	char			m_nValue;
	ComplexListNode*	m_pNext;
	ComplexListNode*	m_pSibling;
}ComplexListNode;

分析：这个问题的重点在于，如何正确的复制m_pSibling这个随机指针。要知道，我们原先复制简单链表的时候，只是关心链表中的m_pNext指针所指向的节点，也就是说，在新的副本链表中，我们只要把各个节点的副本按照m_pNext指针给出的关系串联起来即可。可以说，链表之所以称为链表，就是依赖于m_pNext指针给出的这层拓扑关系。然而随机指针在原链表中并没有严格的先行后续关系，也对链表的拓扑关系没有任何的影响。所以我们如果还是先按m_pNext指针给出的关系复制一个副本链表，再在新的副本链表中找出m_pSibling关系的话，那么每次定位一个节点的m_pSibling指针，就要从原链表及其副本链表的头部开始顺序的找过去。就和原书中描述的一样，这是一个O(N^2)的算法。

问题当然已经得到解决了，但是显然存在优化的空间。下面给出两种思路。

思路1（原书的解法）：就地复制，然后解开（Unwind）两个链表。我们首先设原链表的节点依次为A-B-C...，副本链表的节点依次为a-b-c...。原链表如图1（即下图）所示。

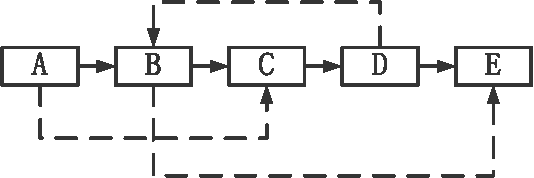
这种思路的具体做法如下所述：

1.对于原链表中的每一个节点A，我们将节点A的副本a放在A的下一个位置，即A->m_pNext为a，并且a->m_pNext为A在原链表中的下一个节点B，这样就可以保持原链表的连续性，维持原链表所依赖的由m_pNext指针提供的拓扑关系，此时我们并未对m_pSibling指针的关系进行复制，但也没有破坏这层关系，如图2（即下图）；

2.随后再参照原链表节点之间的m_pSibling关系，对副本节点进行操作，形成的新链表我们成为纠缠链表，如图3（即下图）；

3.最后从纠缠链表的头部开始遍历，将这个复制后的链表解开，形成两个链表，一个为原链表，另一个就是副本链表，具体的技巧是，第奇数个节点属于原链表，第偶数个节点属于副本链表，如图4（即下图）。

思路1最大的问题不是效率问题，而是安全性问题。如果我们的待复制链表作为一个const的输入参数，那么我们是不能在原先的结构上进行任何更改的。因此我们就需要另外一种方法来解决这种不能原地更改的情况。

思路2：使用一个地址表，第一列存储原链表中每个节点的地址，第二列中存储副本链表中对应的每个节点的地址。具体操作时，可以先按照m_pNext指针给出的关系顺序复制副本链表，并在复制副本链表的过程中，记录下原链表与副本链表中每一个节点的地址，并将其按照一一对应的关系存入地址表的同一行中。在复制结束后，我们再从两个链表的头结点开始遍历，每次遇到不为空的m_pSibling指针时，我们就可以通过查表来找到副本节点应当指向的位置，其实就是将地址表第二列中对应的地址值赋给m_pSibling变量。

这样做的最大问题就是，查表的过程将会直接的影响整个算法的时间复杂度。如果我们只使用简单的二维数组来实现这个地址对应关系表的话，那么每次查表都要消耗O(N)的时间（无论怎么设计这个表）。为了能使查表的时间复杂度尽量降低，我们可以使用哈希的方式来实现这个地址对应关系表，这样做的缺点也是显而易见的，那就是大量的空间开销。

思路讲了半天，下面给出按照两种思路的实现。下面是算法一：

ComplexListNode* Clone_1(ComplexListNode* L){
	ComplexListNode* pCloneList = NULL;

	ComplexListNode* pT = L;
	ComplexListNode* pNew = NULL;
	while(pT != NULL){
		if((pNew = (ComplexListNode*)malloc(sizeof(ComplexListNode))) == NULL) 
			return NULL; //Not safe. Will change the original list in this case.
		pNew->m_nValue = pT->m_nValue + 0x20;
		pNew->m_pSibling = NULL;
		pNew->m_pNext = pT->m_pNext;
		pT->m_pNext = pNew;
		pT = pNew->m_pNext;
	}
	
	pT = L;
	while(pT != NULL){
		pNew = pT->m_pNext;
		if(pT->m_pSibling != NULL)
			pNew->m_pSibling = pT->m_pSibling->m_pNext;
		pT = pNew->m_pNext;
	}

	pT = L;
	pCloneList = L->m_pNext;
	while(pT != NULL){
		pNew = pT->m_pNext;

		//pNew definitely would NOT be NULL now.
		pT->m_pNext = pNew->m_pNext;

		if(pT->m_pNext != NULL)
			pNew->m_pNext = pT->m_pNext->m_pNext;
		
		pT = pT->m_pNext;
		pNew = pNew->m_pNext;
	}

	return pCloneList;
}

　　下面是算法二：

ComplexListNode* Clone_2(const ComplexListNode* L){
	ComplexListNode* pCloneList = NULL;

	const ComplexListNode* pT = L;	
	ComplexListNode* pNew = NULL;
	ComplexListNode* pPre = NULL;
	hash_map<const ComplexListNode*, ComplexListNode*> AddTab;

	//Init the pCloneList, set the Next pointers and fill the AddTab.
	while(pT != NULL){
		if((pNew = (ComplexListNode*)malloc(sizeof(ComplexListNode))) == NULL)
			return NULL;
		
		pNew->m_nValue = pT->m_nValue + 0x20;
		pNew->m_pSibling = NULL;
		pNew->m_pNext = NULL;
		if(pPre == NULL){
			pCloneList = pNew;
		}
		else{
			pPre->m_pNext = pNew;
		}
		pPre = pNew;

		AddTab.insert(pair<const ComplexListNode*, ComplexListNode*>(pT, pNew));

		pT = pT->m_pNext;
	}

	//Set the m_pSibling pointer
	pT = L;
	pNew = pCloneList;
	while(pT != NULL){
		if(pT->m_pSibling != NULL){
			pNew->m_pSibling = AddTab[pT->m_pSibling];
		}

		pT = pT->m_pNext;
		pNew = pNew->m_pNext;
	}

	return pCloneList;
}

　　最后给出一些测试上述算法使用的代码：

#include <stdlib.h>
#include <iostream>
#include <hash_map>

#define LISTLEN 5

using namespace std;
using namespace stdext;

int InitTestList(ComplexListNode** L){
	ComplexListNode* pNewList = NULL;
	if((pNewList = (ComplexListNode*)malloc(sizeof(ComplexListNode) * LISTLEN)) == NULL)
		return 1;
	*L = pNewList;
	ComplexListNode* pT = pNewList;

	//Init Node A
	pT->m_nValue = 0x41;
	pT->m_pNext = &pNewList[1];
	pT->m_pSibling = &pNewList[2];   
	pT = pT->m_pNext;

	//Init Node B
	pT->m_nValue = 0x42;
	pT->m_pNext = &pNewList[2];
	pT->m_pSibling = &pNewList[4];
	pT = pT->m_pNext;

	//Init Node C
	pT->m_nValue = 0x43;
	pT->m_pNext = &pNewList[3];
	pT->m_pSibling = NULL;
	pT = pT->m_pNext;

	//Init Node D
	pT->m_nValue = 0x44;
	pT->m_pNext = &pNewList[4];
	pT->m_pSibling = &pNewList[1];
	pT = pT->m_pNext;

	//Init Node E
	pT->m_nValue = 0x45;
	pT->m_pNext = NULL;
	pT->m_pSibling = NULL;
	
	return 0;
}

void PrintComplexList(const ComplexListNode* L){
	const ComplexListNode* pT = L;
	
	while(pT != NULL){
		cout<<"Value:"<<pT->m_nValue<<"\t";
		if(pT->m_pSibling != NULL)
			cout<<"Sibling:"<<pT->m_pSibling->m_nValue;
		cout<<endl;
		pT = pT->m_pNext;
	}
}

void DestroyTestList(ComplexListNode* L){
	ComplexListNode* pT = L;
	ComplexListNode* pPre = NULL;

	while(pT != NULL){
		pPre = pT;
		pT = pT->m_pNext;
		free(pPre);
	}
}

int main(){
	ComplexListNode* pSrc = NULL;
	ComplexListNode* pDst_1 = NULL;
	ComplexListNode* pDst_2 = NULL;

	if(InitTestList(&pSrc) == 0){
		cout<<"Original List:"<<endl;
		PrintComplexList(pSrc);
		cout<<endl<<endl;

		pDst_1 = Clone_1(pSrc);
		pDst_2 = Clone_2(pSrc);

		cout<<"DestList1 List:"<<endl;
		PrintComplexList(pDst_1);
		cout<<endl<<endl;
		cout<<"DestList2 List:"<<endl;
		PrintComplexList(pDst_2);
		cout<<endl<<endl;

		free(pSrc);//pSrc points to a memory block capable for LISTLEN nodes
		DestroyTestList(pDst_1);
		DestroyTestList(pDst_2);
	}

	return 0;
}

转载于:https://www.cnblogs.com/superpig0501/p/4166019.html