来源:
部分来自wiki:https://en.wikipedia.org/wiki/Coherence_(signal_processing);
部分来自网络其它内容。
The coherence (sometimes called magnitude-squared coherence) between two signals x(t) and y(t) is a real-valued function that is defined as:
where Gxy(f) is the cross-spectral density between x and y, and Gxx(f) and Gyy(f) the autospectral density of x and y respectively. The magnitude of the spectral density is denoted as |G|. Given the restrictions noted above (ergodicity, linearity) the coherence function estimates the extent to which y(t) may be predicted from x(t) by an optimum linear least squares function (最优线性最小二乘函数).
Values of coherence will always satisfy 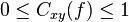 .
.
For an ideal constant parameter linear system with a single input x(t) and single output y(t), the coherence will be equal to one. If Cxy is less than one but greater than zero it is an indication that either: noise is entering the measurements, that the assumed function relating x(t) and y(t) is not linear, or that y(t) is producing output due to input x(t) as well as other inputs. If the coherence is equal to zero, it is an indication that x(t) and y(t) are completely unrelated, given the constraints mentioned above.
The coherence of a linear system therefore represents the fractional part of the output signal power that is produced by the input at that frequency. We can also view the quantity  as an estimate of the fractional power of the output that is not contributed by the input at a particular frequency. This leads naturally to definition of the coherent output spectrum:
as an estimate of the fractional power of the output that is not contributed by the input at a particular frequency. This leads naturally to definition of the coherent output spectrum:
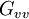 provides a spectral quantification of the output power that is uncorrelated with noise or other inputs.
provides a spectral quantification of the output power that is uncorrelated with noise or other inputs.
一些补充知识:









 本文深入探讨了信号处理领域中共轭的概念,包括其定义、计算方式及实际应用。通过分析共轭在预测线性最小二乘函数、评估系统特性等方面的作用,文章进一步阐述了共轭在理想线性系统中的意义以及与噪声、输入输出关系的关联。同时,通过补充知识部分,详细介绍了共轭在输出功率谱密度量化、无关噪声或输入贡献等方面的量化方法。
本文深入探讨了信号处理领域中共轭的概念,包括其定义、计算方式及实际应用。通过分析共轭在预测线性最小二乘函数、评估系统特性等方面的作用,文章进一步阐述了共轭在理想线性系统中的意义以及与噪声、输入输出关系的关联。同时,通过补充知识部分,详细介绍了共轭在输出功率谱密度量化、无关噪声或输入贡献等方面的量化方法。


















 1911
1911

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








