数学归纳法

数学归纳法对解题的形式要求严格，数学归纳法解题过程中，

第一步：验证n取第一个自然数时成立

第二步：假设n=k时成立，然后以验证的条件和假设的条件作为论证的依据进行推导，在接下来的推导过程中不能直接将n=k+1代入假设的原式中去。

最后一步总结表述。

需要强调是数学归纳法的两步都很重要，缺一不可。

 

例子：举例证明下面的定理

 ——等差数列求和公式

第一步，验证该公式在  n = 1 时成立。即有左边= 1，右边= 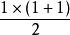  =1，所以这个公式在 n =  1时成立。

第二步，需要证明假设 n =  m 时公式成立，那么可以推导出 n =  m+1 时公式也成立。

步骤如下：

假设 n =  m 时公式成立，即

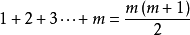   （等式1）

然后在等式两边同时 分别加上 m + 1 得到 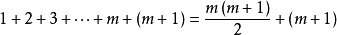  （等式2）

这就是 n =  m+1 时的等式。我们下一步需要根据 等式1证明 等式2 成立。通过因式分解合并，等式2的右边 

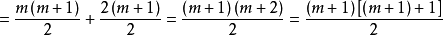
也就是

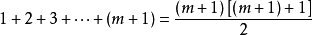
这样我们就完成了由n=m成立推导出n= m+1成立的过程，证毕。

 

结论：对于任意自然数 n，公式均成立。

 

对于以上例子的分析

在这个证明中，归纳的过程如下：

1. 首先证明n=1成立。
2. 然后证明从n=m 成立可以推导出n= m+1 也成立（这里实际应用的是 演绎推理）。
3. 根据上两条从n=1 成立可以推导出n=1+1，也就是n=2 成立。
4. 继续推导，可以知道n=3 成立。
5. 从 n=3 成立可以推导出n=4 也成立……
6. 不断重复3的推导过程（这就是所谓“归纳”推理的地方）。
7. 我们便可以下结论：对于任意非零自然数 n，公式成立。