Buy or Build (poj 2784 最小生成树)

Buy or Build

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 1348		Accepted: 533

Description

World Wide Networks (WWN) is a leading company that operates large telecommunication networks. WWN would like to setup a new network in Borduria, a nice country that recently managed to get rid of its military dictator Kurvi-Tasch and which is now seeking for investments of international companies (for a complete description of Borduria, have a look to the following Tintin albums ``King Ottokar's Sceptre", ``The Calculus Affair" and ``Tintin and the Picaros"). You are requested to help WWN todecide how to setup its network for a minimal total cost.
Problem
There are several local companies running small networks (called subnetworks in the following) that partially cover the n largest cities of Borduria. WWN would like to setup a network that connects all n cities. To achieve this, it can either build edges between cities from scratch or it can buy one or several subnetworks from local companies. You are requested to help WWN to decide how to setup its network for a minimal total cost.

• All n cities are located by their two-dimensional Cartesian coordinates.
  
• There are q existing subnetworks. If q>=1 then each subnetwork c ( 1<=c<=q ) is defined by a set of interconnected cities (the exact shape of a subnetwork is not relevant to our problem).
  
• A subnetwork c can be bought for a total cost wc and it cannot be split (i.e., the network cannot be fractioned).
  
• To connect two cities that are not connected through the subnetworks bought, WWN has to build an edge whose cost is exactly the square of the Euclidean distance between the cities.

You have to decide which existing networks you buy and which edges you setup so that the total cost is minimal. Note that the number of existing networks is always very small (typically smaller than 8).
A 115 Cities Instance
Consider a 115 cities instance of the problem with 4 subnetworks (the 4 first graphs in Figure 1). As mentioned earlier the exact shape of a subnetwork is not relevant still, to keep figures easy to read, we have assumed an arbitrary tree like structure for each subnetworks. The bottom network in Figure 1 corresponds to the solution in which the first and the third networks have been bought. Thin edges correspond to edges build from scratch while thick edges are those from one of the initial networks.

Input

The first line contains the number n of cities in the country ( 1<=n<=1000 ) followed by the number q of existing subnetworks ( 0<=q<=8 ). Cities are identified by a unique integer value ranging from 1 to n . The first line is followed by q lines (one per subnetwork), all of them following the same pattern: The first integer is the number of cities in the subnetwork. The second integer is the the cost of the subnetwork (not greater than 2 x 10 ⁶ ). The remaining integers on the line (as many as the number of cities in the subnetwork) are the identifiers of the cities in the subnetwork. The last part of the file contains n lines that provide the coordinates of the cities (city 1 on the first line, city 2 on the second one, etc). Each line is made of 2 integer values (ranging from 0 to 3000) corresponding to the integer coordinates of the city.

Output

Your program has to write the optimal total cost to interconnect all cities.

Sample Input

7 3
2 4 1 2
3 3 3 6 7
3 9 2 4 5
0 2
4 0
2 0
4 2
1 3
0 5
4 4

Sample Output

17

Hint

Sample Explanation: The above instance is shown in Figure 2. An optimal solution is described in Figure 3 (thick edges come from an existing network while thin edges have been setup from scratch).


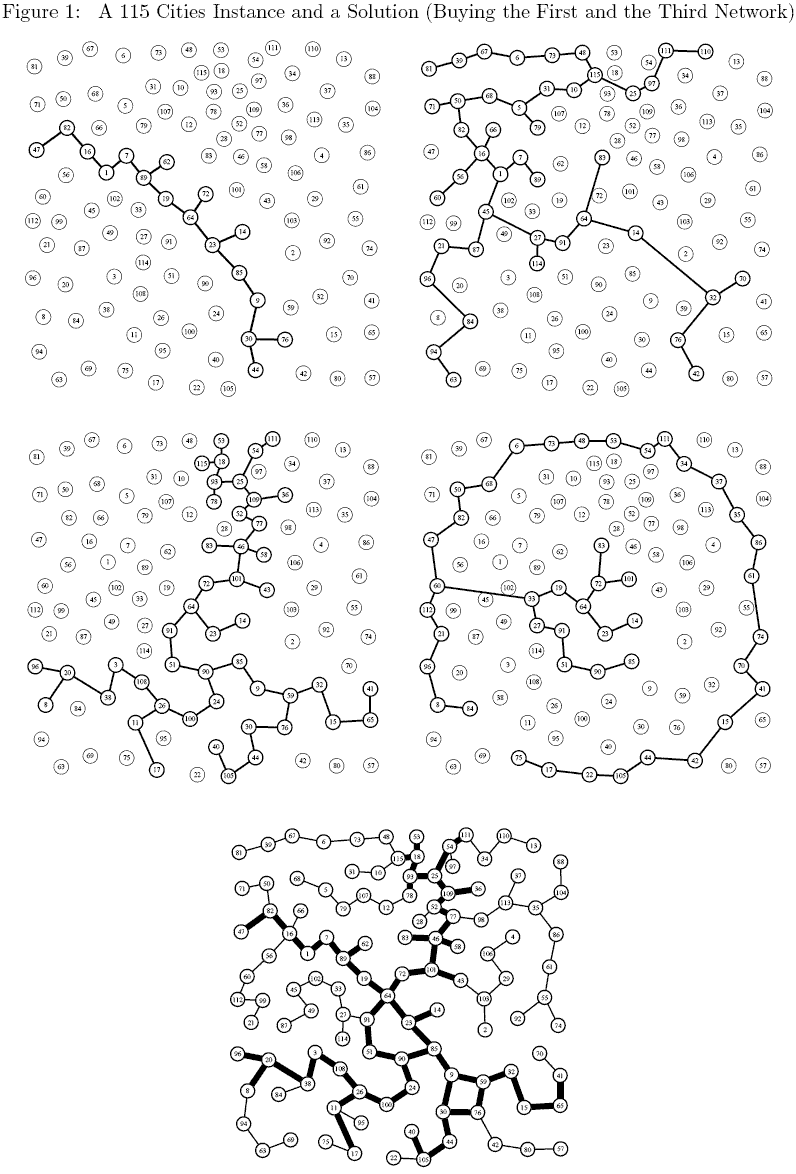
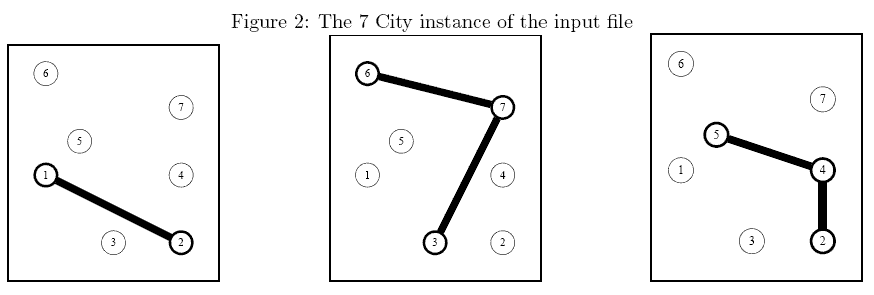
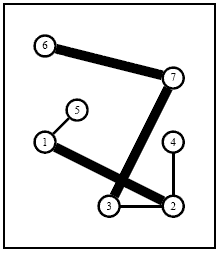
Figure 3: An optimal solution of the 7 City instance in which which the first and second existing networkshave been bought while two extra edges (1, 5) and (2, 4)

Source

Southwestern Europe 2005

题意：n个城市，告诉每一个城市的坐标，还有q个联通块，如今要把这n个城市连起来，能够购买联通块（每一个有一定的费用），或者新建一条边（费用为点之间的距离的平方）。问最小费用是多少。

思路：q非常小。二进制枚举选哪些块。每次kruskal一遍，求最小值。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#pragma comment (linker,"/STACK:102400000,102400000")
#define mod 1000000009
#define INF 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-6
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define FRE(i,a,b)  for(i = a; i <= b; i++)
#define FREE(i,a,b) for(i = a; i >= b; i--)
#define FRL(i,a,b)  for(i = a; i < b; i++)
#define FRLL(i,a,b) for(i = a; i > b; i--)
#define mem(t, v)   memset ((t) , v, sizeof(t))
#define sf(n)       scanf("%d", &n)
#define sff(a,b)    scanf("%d %d", &a, &b)
#define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c)
#define pf          printf
#define DBG         pf("Hi\n")
typedef long long ll;
using namespace std;

const int maxn = 1005;
const int MAXN = 500500;

struct Node
{
    int x,y;
}node[maxn];

struct Edge
{
    int u,v,len;
    bool operator<(const Edge &a)const
    {
        return len<a.len;
    }
}edge[MAXN];

int father[maxn],cost[10];
int n,q,num;
vector<int>g[10];

void init()
{
    for (int i=0;i<=n;i++)
        father[i]=i;
}

void addedge(int u,int v)
{
    edge[num].u=u;
    edge[num].v=v;
    edge[num++].len=(node[u].x-node[v].x)*(node[u].x-node[v].x)+(node[u].y-node[v].y)*(node[u].y-node[v].y);
}

int find_father(int x)
{
    if (x!=father[x])
        father[x]=find_father(father[x]);
    return father[x];
}

bool Union(int a,int b)
{
    int fa=find_father(a);
    int fb=find_father(b);
    if (fa==fb) return false;
    father[fa]=fb;
    return true;
}

int Kruskal()
{
    int ans=0;
    int cnt=0;
    for (int i=0;i<num;i++)
    {
        if (Union(edge[i].u,edge[i].v))
        {
            ans+=edge[i].len;
            cnt++;
        }
        if (cnt==n-1) break;
    }
    return ans;
}

void solve()
{
    init();
    int ans=Kruskal();
    for (int i=0;i<(1<<q);i++)
    {
        init();
        int all=0;
        for (int j=0;j<q;j++)
        {
            if (!((i>>j)&1)) continue;
            all+=cost[j];
            for (int k=1;k<g[j].size();k++)
                Union(g[j][k],g[j][0]);
        }
        ans=min(ans,all+Kruskal());
    }
    pf("%d\n",ans);
}

int main()
{
    int i,j,t,number,x;
//    sf(t);
//    while (t--)
    {
        sff(n,q);
        num=0;
        for (i=0;i<q;i++)
        {
            g[i].clear();
            sff(number,cost[i]);
            for (j=0;j<number;j++)
            {
                sf(x);
                g[i].push_back(x);
            }
        }
        for (i=1;i<=n;i++)
            sff(node[i].x,node[i].y);
        for (i=1;i<=n;i++)
            for (j=i+1;j<=n;j++)
                addedge(i,j);
        sort(edge,edge+num);
        solve();
//        if (t) puts("");
    }
    return 0;
}
/*
1

7 3
2 4 1 2
3 3 3 6 7
3 9 2 4 5
0 2
4 0
2 0
4 2
1 3
0 5
4 4
*/

转载于:https://www.cnblogs.com/yutingliuyl/p/6878266.html