A field guide to algebra,theorem 1.1.3

Let $\sum$ be a subset of $\mathbf{R}$ containing $0$ and $1$,the set $E(\sum)$ of all real numbers which are constructable from $\sum$ satisfies the following properties:

 

  a):if $x,y\in E(\sum)$ ,then $x+y,x-y,xy,$ and $\frac{x}{y}\in E(\sum)$ if $y\neq 0$. 

  b):if $x>0$, $x\in E(\sum)$,then $\sqrt{x}\in   E(\sum)$.

  Proof:

  a)Construction of $x+y$: $\frac{x+y}{2}$ can be constructed by taking the midpoint of $x$ and $y$(It is easy to verify that a midpoint can be constructed by drawing two circles of radius $|x-y|$ which centering at $x$ and $y$ respectively.Then drawing a line passing through the two intersection points of the circles.Then this passing line intersects with the line passing though $x$ and $y$,the intersection point is $\frac{x+y}{2}$.).Then $x+y$ can be constructed by drawing a circle centering at $\frac{x+y}{2}$ with radius $\frac{|x+y|}{2}$.


  Construction of $x-y$:$-y$ can be constructed by drawing a circle  centering at $0$ with radius $|y|$. $x+(-y)$ can be constructed,so
  $x-y$ can be constructed.
 

  Construction of $xy$:In the plane $\mathbf{R}^2$,$(x-1,0)$ can be  constructed.So the point $(x-1,y)$ can be easily
  constructed(Why?)The intersection point of the line $y'-0=y(x'-x)$  and $x'=0$ is $(0,-xy)$.So $xy$ can be constructed easily.


  Construction of $\frac{1}{y}$ if $y\neq 0$:In the plane  $\mathbf{R}^2$,$(x-xy,0)$ can be easily constructed.$(x-xy,1)$ can  be easily constructed.The intersection point of the line  $y'-0=\frac{1}{xy}(x'-x)$ and $x'=0$ is $\frac{-1}{y}$.So  $\frac{1}{y}$ can be easily constructed.



  b):In $\mathbf{R}^2$,a line $y'=kx'+c$,a circle  $(x'-a)^2+(y'-b)^2=r^2$.$r>0,k,c\in\mathbf{R}$.Let the intersection  point be $(m,n)$,then
  \begin{equation}
    \label{eq:22_11_48}
    (1+k^2)m^2+[2(c-b)k-2a]m+[a^2+(c-b)^2-r^2]=0
  \end{equation}
  Then
  \begin{equation}
    \label{eq:22_11_50}
    m=\frac{-[2(c-b)k-2a]\pm \sqrt{\Delta}}{2(1+k^2)}  
  \end{equation}
  It is a delight to see that a $\sqrt{}$ appears in  \ref{eq:22_11_50}.$\Delta  =[2(c-b)k-2a]^2-4(1+k^2)[a^2+(c-b)^2-r^2]$. Let $k=0$,then
  \begin{equation}
    \label{eq:22_16_04}
    m=\frac{2a\pm \sqrt{4r^2-4(c-b)^2}}{2}=a\pm \sqrt{r^2-(c-b)^2}
  \end{equation}

Let $r^2-(c-b)^2=x$.For example,let $c=b$,and $r=x$,then
\begin{equation}
  \label{eq:22_16_15}
  m=a\pm \sqrt{x}
\end{equation}
So $\sqrt{x}$ is constructed.$\Box$

Remark:冬眠的老鼠(哆嗒数学QQ群(128709478)里的一个比较牛的人)has an alternative way of constructing $\sqrt{x}$，by using the power of a point.See the below picture.

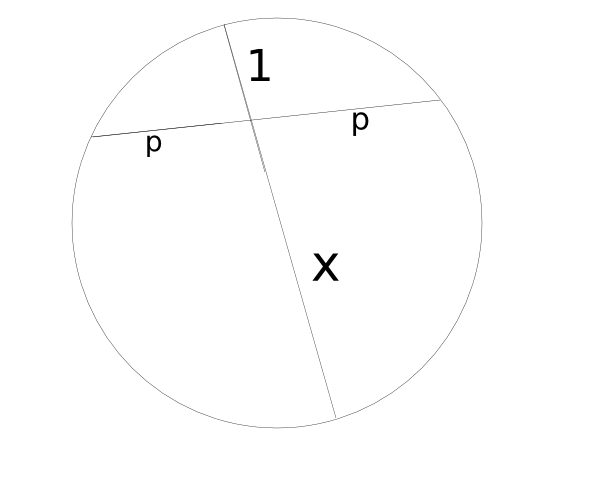$p^2=1x$,So $p=\sqrt{x}$.So $\sqrt{x}$ is constructed.

转载于:https://www.cnblogs.com/yeluqing/archive/2012/09/22/3827976.html