吴恩达Coursera机器学习 - Chapter 4 多变量线性回归

Chapter 4 – 多变量线性回归(Linear Regression with Multiple Variables)

相比第二章，这一章无非就是数据集的特征数由一个变为多个，并引入了矩阵的概念。在第二章和高等数学的基础上，学起来也挺快的。

多变量的线性回归

• 新的假设函数

  这里我们引入新的变量n（$n \geq 2$），代表模型/函数的变量数目。

$$ h\left( x \right) = \theta^{T}X = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + \ldots + \theta_{n}x_{n} $$

• 代价函数的表示没变
• 梯度下降函数的表示也没变，但要提一提

  由于h(x)的改变，求导后梯度下降算法变为：
  
  如此循环直至收敛。
  以n=2为例，大括号内可写作：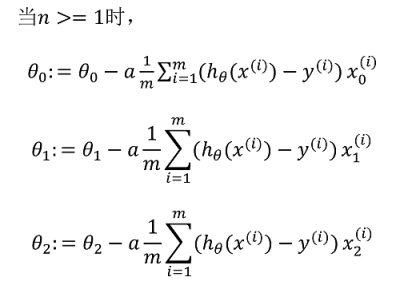
  
  对了，$x_0$就是1，加进来是为了统一。

特征缩放

保持特征值有相近的尺度将使$J\left( \theta_{0},\ \theta_{1}\right)$更快收敛。当数据的各特征值不在一个量级时，我们可以将他们的尺度缩放到-1~1之间。

最简单的方法是令：$x_{n} = \frac{x_{n} -\mu_{n}}{s_{n}}$，其中$\mu_{n}$为平均值，$s_{n}$为标准差。

多项式回归

线性回归并不适用于所有数据，有时可能用到二次方或三次方模型。这种情况下，先观察数据再决定尝试什么样的模型。有种方法是这样的，如：令$x_{2}= x_{2}^{2},\ x_{3} = x_{3}^{2}$，从而将二次方模型转化为线性模型

正规方程

• 原理：求解$\frac{\partial}{\partial\theta_{j}}J\left( \theta_{j}\right) = 0$
• 正规方程表示：$\theta = {(X^{T}X)}^{- 1}X^{T}y$
  其中X为训练集的特征矩阵，y为目标变量的矢量

注意：线性代数中，定义方阵可逆的充分必要条件为方阵的行/列向量线性无关，因此，若特征之间不独立或特征数量大于训练集数量，正规方程无法使用。（后面所学的正则化方法可以在大量特征值和少量样本的情况下，依然能求解θ）

• 正规方程与梯度下降算法的比较

正规方程	梯度下降
不需要多余参数	需要选择学习率α
一次计算完成	需要多次迭代
矩阵逆计算的时间复杂度为$O(n^{3})$ 适合n较小的情况，一般n<10000	特征数量n较大时适用
仅适用于线性模型	适用各种类型的模型