①活动安排问题
设有N个活动时间集合,每个活动都要使用同一个资源,比如说会议场,而且同一时间内只能有一个活动使用,每个活动都有一个使用活动的开始si和结束时间fi,即他的使用区间为(si,fi),现在要求你分配活动占用时间表,即哪些活动占用该会议室,哪些不占用,使得他们不冲突,要求是尽可能多的使参加的活动最大化,即所占时间区间最大化!
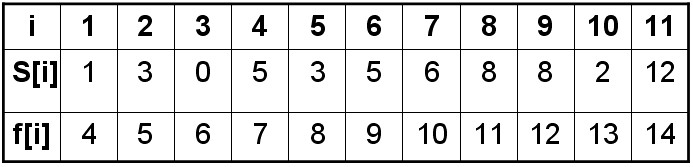
上图为每个活动的开始和结束时间,我们的任务就是设计程序输出哪些活动可以占用会议室!
#include <iostream>
using namespace std;
void GreedyChoose(int len,int *s,int *f,bool *flag);
int main(int argc, char* argv[])
{
int s[11] ={1,3,0,5,3,5,6,8,8,2,12};
int f[11] ={4,5,6,7,8,9,10,11,12,13,14};
bool mark[11] = {0};
GreedyChoose(11,s,f,mark);
for(int i=0;i<11;i++)
if(mark[i])
cout<<i<<" ";
system("pause");
return 0;
}
void GreedyChoose(int len,int *s,int *f,bool *flag)
{
flag[0] = true;
int j = 0;
for(int i=1;i<len;++i)
if(s[i] >= f[j])
{
flag[i] = true;
j = i;
}
}
问题分析
1:假设我们已经安排了一些活动,那么我们想要使后面的活动尽可能的安排的多,则要使前面的活动尽量早的结束
2:根据上面的策略,我们安排活动的时候就要安排时间早的,只有结束时间早才有可能尽量多的在后面安排活动。
思路搭建
1:排序问题。因为给的活动的结束和开始时间是没有顺序的,所以我们要按照结束时间从小到大排序
2:选择问题。选择开始最早的活动,以这个活动的结束时间寻找下一个活动,再以下一个活动的结束时间为标准,再向下找,直至结束。
②.贪心实例之线段覆盖
题目大意:
在一维空间中告诉你N条线段的起始坐标与终止坐标,要求求出这些线段一共覆盖了多大的长度。

为了方便说明,我们采用上述表格中的数据代表10条线段的起始点和终点,注意,这里是用起始点为顺序进行排列,和上面的不一样,知道了这些我们就可以着手开始设计这个程序:
#include <iostream>
using namespace std;
int main(int argc, char* argv[])
{
int s[10] = {2,3,4,5,6,7,8,9,10,11};
int f[10] = {3,5,7,6,9,8,12,10,13,15};
int TotalLength = (3-2);
for(int i=1,int j=0; i<10 ; ++i)
{
if(s[i] >= f[j])
{
TotalLength += (f[i]-s[i]);
j = i;
}
else
{
if(f[i] <= f[j])
continue;
else
{
TotalLength += f[i] - f[j];
j = i;
}
}
}
cout<<TotalLength<<endl;
system("pause");
return 0;
}
③数字组合问题
设有N个正整数,现在需要你设计一个程序,使他们连接在一起成为最大的数字,例3个整数 12,456,342 很明显是45634212为最大,4个整数 342,45,7,98显然为98745342最大
程序要求:输入整数N 接下来一行输入N个数字,最后一行输出最大的那个数字!
题目解析:拿到这题目,看起要来也简单,看起来也难,简单在什么地方,简单在好像就是寻找哪个开头最大,然后连在一起就是了,难在如果N大了,假如几千几万,好像就不是那么回事了,要解答这个题目需要选对合适的贪心策略,并不是把数字由大排到小那么简单,网上的解法是将数字转化为字符串,比如a+b和b+a,用strcmp函数比较一下就知道谁大,也就知道了谁该排在谁前面,不过我觉得这个完全没必要,在这里我采用一种比较巧妙的方法来解答,不知道大家还记得冒泡排序法不,那是排序最早接触的一种方法,我们先看看它的源代码:
#include <iostream>
using namespace std;
int main(int argc, char* argv[])
{
int array[10];
for(int i=0;i<10;i++)
cin>>array[i];
int temp;
for(i=0; i<=9 ; ++i)
for(int j=0;j<10-1-i;j++)
if(array[j] > array[j+1] )
{
temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
for(i=0;i<10;i++)
cout<<array[i]<<" ";
cout<<endl;
system("pause");
return 0;
相信这种冒泡已经很熟悉了,注意看程序中最核心的比较规则是什么,是这一句if(array[j] > array[j+1] ) 他是以数字大小作为比较准则来返回true或者是false,那么我们完全可以改变一下这个排序准则,比如23,123,这两个数字,在我们这个题中它可以组成两个数字 23123和12323,分明是前者大些,所以我们可以说23排在123前面,也就是23的优先级比123大,123的优先级比23小,所以不妨写个函数,传递参数a和b,如果ab比ba大,则返回true,反之返回false,函数原型如下:
bool compare(int Num1,int Num2)
{
int count1,count2;
int MidNum1 = Num1,MidNum2 = Num2;
while( MidNum1 )
{
++count1;
MidNum1 /= 10;
}
while( MidNum2 )
{
++count2;
MidNum2 /= 10;
}
int a = Num1 * pow(10,count2) + Num2;
int b = Num2 * pow(10,count1) + Num1;
return (a>b)? true:false;
}
好了,我们的比较准则函数也已经完成了,只需要把这个比较准则加到关键的地方,这个题就算完成了,最终代码如下:
#include <iostream>
#include <cmath>
using namespace std;
bool compare(int Num1,int Num2);
int main(int argc, char* argv[])
{
int N;
cout<<"please enter the number n:"<<endl;
cin>>N;
int *array = new int [N];
for(int i=0;i<N;i++)
cin>>array[i];
int temp;
for(i=0; i<=N-1 ; ++i)
{
for(int j=0;j<N-i-1;j++)
if( compare(array[j],array[j+1]) )
{
temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
cout<<"the max number is:";
for( i=N-1 ; i>=0 ; --i)
cout<<array[i];
cout<<endl;
delete [] array;
system("pause");
return 0;
}
bool compare(int Num1,int Num2)
{
int count1=0,count2=0;
int MidNum1 = Num1,MidNum2 = Num2;
while( MidNum1 )
{
++count1;
MidNum1 /= 10;
}
while( MidNum2 )
{
++count2;
MidNum2 /= 10;
}
int a = Num1 * pow(10,count2) + Num2;
int b = Num2 * pow(10,count1) + Num1;
return (a>b)? true:false;
}
可以看见这样很巧妙的改编冒泡排序就解决了这个问题,当然也可以用其他的排序算法,或者干脆用一个仿函数作为set容器的排序准则,insert进去就可以了,但是这个程序有一点小问题,假如输入的数字中有两个濒临越界的数据,合并在一起就越界了,那样就只能用字符串的形式进行比较!
④ :找零钱的问题
在贪心算法里面最常见的莫过于找零钱的问题了,题目大意如下,对于人民币的面值有1元 5元 10元 20元 50元 100元,下面要求设计一个程序,输入找零的钱,输出找钱方案中最少张数的方案,比如123元,最少是1张100的,1张20的,3张1元的,一共5张!
解析:这样的题目运用的贪心策略是每次选择最大的钱,如果最后超过了,再选择次大的面值,然后次次大的面值,一直到最后与找的钱相等,这种情况大家再熟悉不过了,下面就直接看源代码:
#include <iostream>
#include <cmath>
using namespace std;
int main(int argc, char* argv[])
{
int MoneyClass[6] = {100,50,20,10,5,1}; //记录钱的面值
int MoneyIndex [6] ={0}; //记录每种面值的数量
int MoneyAll,MoneyCount = 0,count=0;
cout<<"please enter the all money you want to exchange:"<<endl;
cin>>MoneyAll;
for(int i=0;i<6;) //只有这个循环才是主体
{
if( MoneyCount+MoneyClass[i] > MoneyAll)
{
i++;
continue;
}
MoneyCount += MoneyClass[i];
++ MoneyIndex[i];
++ count;
if(MoneyCount == MoneyAll)
break;
}
for(i=0;i<6;++i) //控制输出的循环
{
if(MoneyIndex[i] !=0 )
{
switch(i)
{
case 0:
cout<<"the 100 have:"<<MoneyIndex[i]<<endl;
break;
case 1:
cout<<"the 50 have:"<<MoneyIndex[i]<<endl;
break;
case 2:
cout<<"the 20 have:"<<MoneyIndex[i]<<endl;
break;
case 3:
cout<<"the 10 have:"<<MoneyIndex[i]<<endl;
break;
case 4:
cout<<"the 5 have:"<<MoneyIndex[i]<<endl;
break;
case 5:
cout<<"the 1 have:"<<MoneyIndex[i]<<endl;
break;
}
}
}
cout<<"the total money have:"<<count<<endl;
system("pause");
return 0;
}
⑤加油站问题
一辆汽车加满油可以行驶n千米,路途中有若干个加油站,为了使沿途加油次数最少,设计一个算法,输出最好的加油方案。
假如:假设沿途有9个加油站,总路程为100千米,加满油后汽车行驶的最远距离为20千米,汽车加油的位置分别距离起点10,20,35,40,50,65,75,85,90.
分析:
(1)第一次汽车从起点出发,行驶到n=20千米时,选择一个距离终点最近的加油站Xi,应选择距离起点为20千米的加油站。
(2)加完一次油时,汽车处于满油状态,这与汽车出发之前的状态一致,这样就将问题归结为求Xi到终点汽车加油次数最少的一个规模最小的子问题。
按照以上策略不断的解决子问题,即每次找到从前一次选择的加油站开始往前几千米之间,距离终点最近的加油站加油。
#include<stdio.h>
#define S 100
int main()
{
int i,j,n,k=0,total,dist;
int x[]={10,20,35,40,50,65,75,85,100};//加油站距离起点的位置
int a[10];//选择加油站的位置
n=sizeof(x)/sizeof(x[0]);//加油站的个数
printf("请输入最远行车距离(15<=n<=100):");
scanf("%d",&dist);
total=dist; //初始化刚开始时能行驶的最远距离
j=1; //选择的加油站个数
while(total<S)//如果汽车没有走完全程
{
for(i=k;i<n;i++)
{
if(x[i]>total)//如果距离下一站太远
{
a[j]=x[i-1];//则在当前加油点加油
j++;
total=x[i-1]+dist;//计算加完油能行驶
k=i;//记录下一次加油的开始位置
break;
}
}
}
for(i=1;i<j;i++) //输出选择的加油点
{
printf("%4d",a[i]);
}
printf("\n");
return 0;
}
⑥HDU贪心题解
解法1:
这里用冒泡排序完成
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
int a,b,c,i,l;
double sum;
int j[1010],f[1010];
double k[1010],d;
while(scanf("%d%d",&a,&b)!=EOF)
{
if(a==-1&&b==-1)break;
sum=0;
for(i=0;i<b;i++)
{
cin>>j[i]>>f[i];
k[i]=j[i]*1.0/f[i];
}
for(i=0;i<b;i++)
{
for(l=i;l<b-i-1;l++)
{
if(k[l]>k[l+1])
{
c=j[l];j[l]=j[l+1];j[l+1]=c;
c=f[l];f[l]=f[l+1];f[l+1]=c;
d=k[l];k[l]=k[l+1];k[l+1]=d;
}
}
}
int temp=a;
for(i=b-1;i>=0;i--)
{
temp=temp-f[i];
if(temp>=0) sum=sum+j[i];
else
{
sum=sum+(temp+f[i])*k[i];
break;
}
}//排完序如何计算也是关键
printf("%.3f\n",sum);
}
return 0;
}
解法2:
#include<iostream>
#include<algorithm>
using namespace std;
struct Node
{
double j,f,p;
}node[1000];
int cmp(Node x,Node y)
{
return x.p>y.p;
}
int main()
{
int n,m;
while(scanf("%d%d",&n,&m)!=EOF&&(m!=-1||n!=-1))
{
double sum=0;
int i;
for(i=0;i<m;i++)
{
scanf("%lf%lf",&node[i].j,&node[i].f);
node[i].p=node[i].j/node[i].f;
}
sort(node,node+m,cmp);
for(int i=0;i<m;i++)
{
if(node[i].f<n)
{
sum=sum+node[i].j;
n=n-node[i].f;
}
else
{
sum=sum+node[i].p*n;
break;
}
}
printf("%.3lf\n",sum);
}
return 0;
}
























 480
480

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








