Divide and Conquer 实例

最新推荐文章于 2025-09-08 09:22:18 发布

weixin_34151004

最新推荐文章于 2025-09-08 09:22:18 发布

阅读量174

点赞数

CC 4.0 BY-SA版权

文章标签： python

原文链接：https://my.oschina.net/zjuysw/blog/190828

本文深入探讨了分治算法的基本概念、运行时间分析，并通过具体实例如最大子序列和问题、排序算法等展示了其在解决复杂问题时的高效性。此外，还详细介绍了分治算法在解决最近点问题和选择问题上的应用，以及如何优化整数乘法和矩阵乘法。文章旨在为读者提供全面理解分治策略和技术的指南。

2019独角兽企业重金招聘Python工程师标准>>>

Algorithm Design Techniques - 2

##Divide and Conquer##

note:

Divide : smaller problem are solved recursively (except base cases)

Conquer : The solution to the original problem is then formed from the solutions to the sub-problems.

###Cases solved by divide and conquer###

The maximum sub-sequence sum – the O( N log N ) solution
The maximum sub-sequence sum – the O( N log N ) solution
Merge-sort and quick-sort – O( N log N )

###Running Time of Divide and Conquer Algorithms###

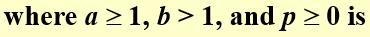
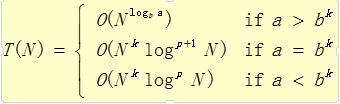
merge-sort : a = b = 2; p = 0 and k = 1; ---> T = O(N*logN)

中文解释

####Closest Points Problem####

问题描述：平面上有n个点，找到距离最短的两个点。

<!-- lang: cpp -->
/* points are all in the strip */
for ( i=0; i<NumPointsInStrip; i++ )
    for ( j=i+1; j<NumPointsInStrip; j++ ) 
        if ( Dist( Pi , Pj ) < min )
	         min = Dist( Pi , Pj );
/* points are all in the strip */
/* and sorted by y coordinates */
for ( i = 0; i < NumPointsInStrip; i++ )
    for ( j = i + 1; j < NumPointsInStrip; j++ ) 
        if ( Dist_y( Pi , Pj ) > min )
	        break;
        else  if ( Dist( Pi , Pj ) < min )
	        min = Dist( Pi , Pj );

####The Selection Problem####

####Multiplying Integers####

####Matrix Multiplication####

转载于:https://my.oschina.net/zjuysw/blog/190828