2017年2月17日 Gaussian Naive Bayes

朴素贝叶斯分类器

最新推荐文章于 2025-09-11 23:49:31 发布

weixin_34150503

最新推荐文章于 2025-09-11 23:49:31 发布

阅读量127

点赞数

CC 4.0 BY-SA版权

文章标签：人工智能 python

原文链接：https://my.oschina.net/airxiechao/blog/862753

本文介绍了一种基于高斯分布的朴素贝叶斯分类器实现，并使用鸢尾花数据集进行演示。该分类器假设特征间相互独立，并采用高斯分布估计特征的似然概率。

2019独角兽企业重金招聘Python工程师标准>>>

Naive Bayes method is based on applying Bayes’s theorm with the “naive” assumption of independence between features

Gaussian Naive Bayes assumes the likelihood is gaussian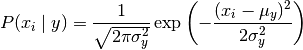

from __future__ import division
import numpy as np
from sklearn.naive_bayes import GaussianNB
from scipy.stats import norm
from sklearn.datasets import load_iris
from pylab import scatter, show, legend, xlabel, ylabel

data = load_iris()
X = data.data
y = data.target

def visualize(X, y):
    ys = np.unique(y)
    for v in ys:   
        pos = np.where(y == v)
        scatter(X[pos, 0], X[pos, 1])
    show()

visualize(X, y)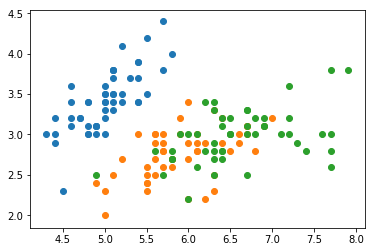

class myGaussianNB:
    def fit(self, X, y):
        self.pys = {}
        for v in np.unique(y):
            self.pys[v] = y[y==v].shape[0] / y.shape[0]

        self.pxys = {}
        for v in np.unique(y):
            for i in range(X.shape[1]):
                xs = X[y==v]
                x_mean = np.mean(xs[:,i])
                x_std = np.std(xs[:,i])
                self.pxys[(v,i)] = (x_mean, x_std)
                
    def predict_single(self, x):
        ps = [ self.pys[v] * np.sum([ norm.pdf(x[i], self.pxys[(v,i)][0], self.pxys[(v,i)][1]) for i in range(X.shape[1])]) for v in np.unique(y)]
        return np.unique(y)[np.argmax(ps)]
    
    def predict(self, X):
        return np.array(map(self.predict_single, X))
    
    def score(self, X, y):
        res = self.predict(X)
        return np.count_nonzero((res == y) == True) / y.shape[0]
    
nb = myGaussianNB()
nb.fit(X, y)
print 'score:',nb.score(X, y)
#score: 0.953333333333

转载于:https://my.oschina.net/airxiechao/blog/862753