K-means clustering aims to partition the samples into k sets so as to miniize the sum of distances between each pointer to the K center
The algorithm proceeds by iterating two steps: cluster assignment step and center update step, until assignments no longer change.
from __future__ import division
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline
data = load_iris()
X = data.data
y = data.target
class myKMean:
def compute_centers(self, X, predict, n_clusters):
centers = []
for c in range(n_clusters):
centers.append(np.mean(X[np.where(predict == c)], axis=0))
return np.array(centers)
def compute_cluster(self, X, centers):
predict = []
for x in X:
distances = [ np.sqrt(np.sum((x-c)**2)) for c in centers]
predict.append(np.argmin(distances))
return np.array(predict)
def fit(self, X, n_clusters):
predict = np.random.randint(n_clusters, size=X.shape[0])
while True:
self.centers = self.compute_centers(X, predict, n_clusters)
p = self.compute_cluster(X, self.centers)
if np.count_nonzero(predict - p) == 0:
break
else:
predict = p
def predict(self, X):
return self.compute_cluster(X, self.centers)
km = myKMean()
km.fit(X, len(np.unique(y)))
for i in range(data.target_names.shape[0]):
Xi = X[np.where(y == i)]
plt.scatter(Xi[:,0], Xi[:,1])
plt.scatter(km.centers[:,0], km.centers[:,1], marker='x')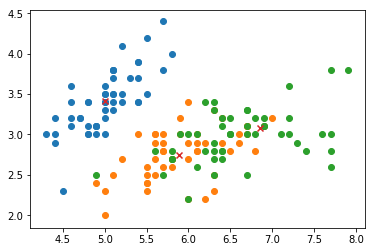







 本文介绍了一种K-means聚类算法的实现过程,包括样本分配和中心更新两个迭代步骤,直至分配不再变化。通过使用Python和NumPy库,文章展示了如何从鸢尾花数据集中加载数据,并进行聚类分析。
本文介绍了一种K-means聚类算法的实现过程,包括样本分配和中心更新两个迭代步骤,直至分配不再变化。通过使用Python和NumPy库,文章展示了如何从鸢尾花数据集中加载数据,并进行聚类分析。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








