斑点检测(LoG,DoG)(下)

最新推荐文章于 2024-11-11 10:17:53 发布
转载 最新推荐文章于 2024-11-11 10:17:53 发布 · 613 阅读 · 5 ·
CC 4.0 BY-SA版权
原文链接：http://www.cnblogs.com/YiXiaoZhou/p/5892083.html
文章标签：

#python #人工智能

本文深入探讨了基于二阶导数过零点的斑点检测原理，解析了从边缘检测到斑点检测的变化，并介绍了如何通过尺度归一化选择合适的检测尺度。此外，还对比了LoG与DoG算子的区别及联系。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

斑点检测(LoG,DoG)(下)

LoG， DoG， 尺度归一化

上篇文章斑点检测(LoG,DoG)(上)介绍了基于二阶导数过零点的边缘检测方法，现在我们要探讨的是斑点检测。在边缘检测中，寻找的是二阶导数的零点，可是在斑点检测中寻找的是极值点，这是为什么呢？而且在使用二阶导数寻找斑点时不仅在图像上寻找极值点，还要求在尺度空间上也是极值点，又是为什么呢？还有为什么DoG是LoG的简化版本呢？？

这篇文章主要内容就是回答这三个问题。

From edges to blobs

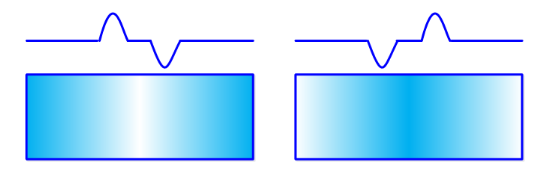
对于阶跃信号，其二阶导数在对应跃变得位置会产生一个波，该波的过零点正对应着待检测的边缘位置。

enter description here

1474424864226.jpg

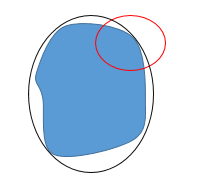
而所谓的斑点区域就是两条边形成的中间区域，如下图中，对于蓝色的目标区域，红色的椭圆就是在检测边缘，黑色的椭圆就是在检测斑点区域。

enter description here

1474425468660.jpg

那么边缘检测到斑点检测的过程对二阶导数有什么影响呢？

enter description here

1474425595728.jpg

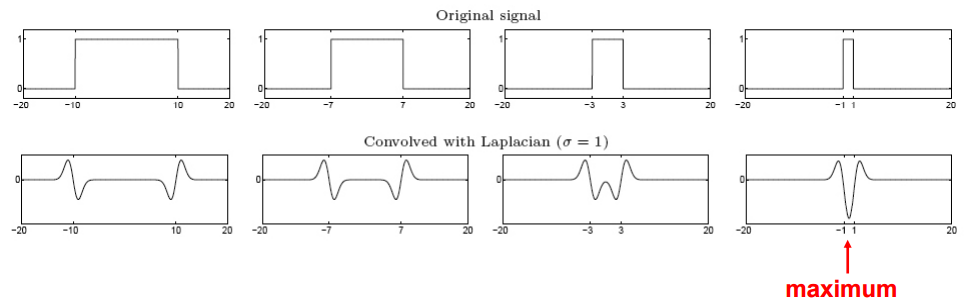
这个示意图中上一行从左到右表示的是原始矩形脉冲信号，脉冲信号的周期越来越短，而下一行则表示对应周期在相同尺度下的LoG结果。可以发现总的LoG曲线其实是两条边界上产生的LoG函数的叠加，当两条边界足够小时，在该尺度脉冲下就被作为了blob，这时候LoG曲线的极值就对应着blob的中心。

所以边缘检测对应的是LoG的过零点，而斑点检测对应的是LoG的极值点。

这里我们可以发现判断是不是blob时，尺度非常重要，只有尺度大于一定值得时候blob才可以通过LoG的极值判定。

那么尺度该如何选择呢？

尺度的选择

先来看看同一个阶跃信号在不同尺度下的响应

enter description here

1474426170925.jpg

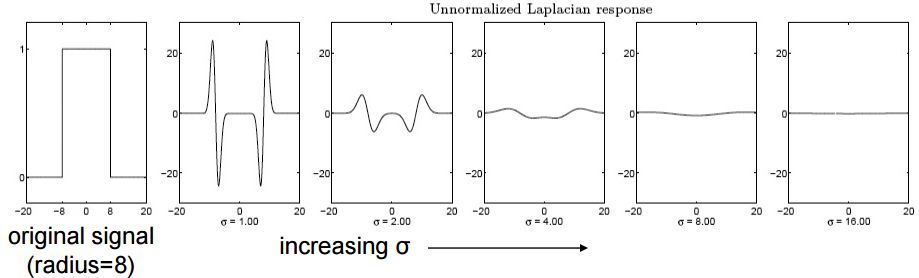
可以发现随着尺度的不断增大，LoG曲线由双波谷逐渐融合成单波谷，但是响应的幅值越来越弱。这是因为，随着尺度的增大，LoG算子的最大幅度逐渐减小，导致响应也随着尺度的增大而减小。

这种情况我们没法知道选定的尺度是否合适，进而不知道这个尺度下找到的极值点是不是对应着blob的中心点，万一是边缘产生波的极值点怎么办！所以我们这时候应该对进行LoG算在进行尺度的归一化。

下图给出了阶跃信号的一阶Gaussian滤波曲线

enter description here

1474426585595.jpg

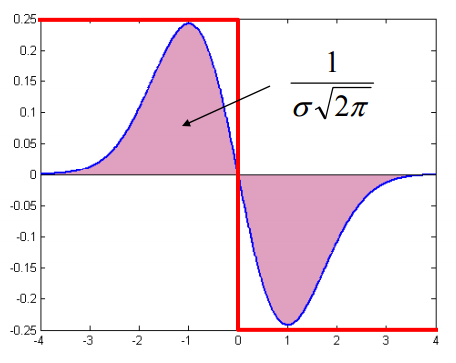
可以发现对于稳定信号，响应的最大幅值是和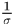1027162-20160921114129871-16663004.png成正比的，那么为了消除尺度的影响，可以对一阶高斯滤波算子乘上个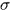1027162-20160921114130231-189871151.png,那么对于不同的尺度，其响应的强度就是相同的了。这里可以这么理解，在0点处积分结果为

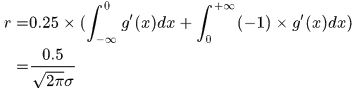
1027162-20160921114130809-1658521344.png

是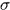1027162-20160921114131387-156774251.png的函数表示与尺度有关，乘上一个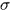1027162-20160921114131902-433226037.png之后就与尺度无关了，称为尺度的归一化。

而LoG算子是Gaussian 滤波的二阶导数，所以应该乘上个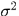1027162-20160921114132356-1648096182.png做尺度归一化。

再来看看矩形脉冲在不同尺度经过尺度归一化后的响应

enter description here

1474427171097.jpg

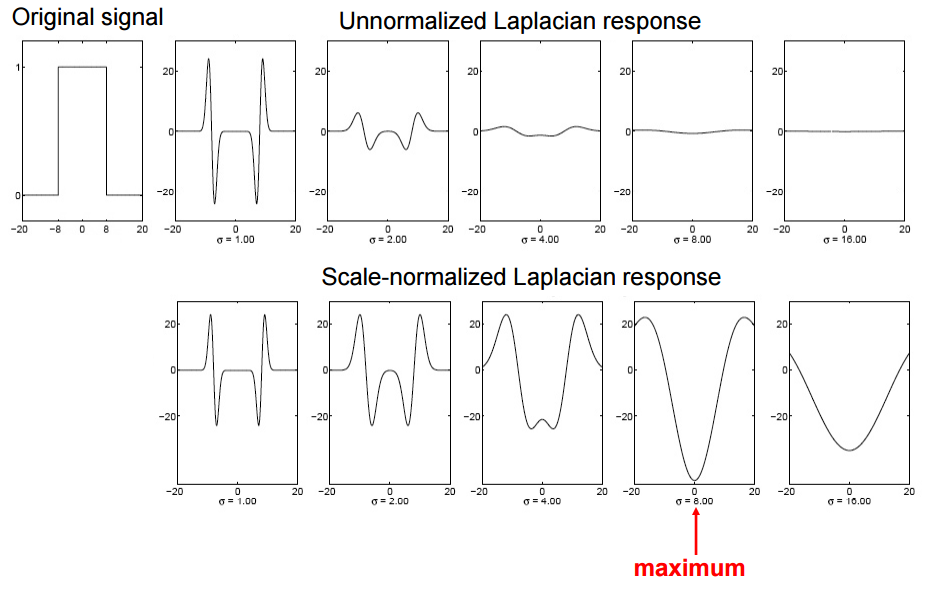
可以发现当尺度等于脉冲宽度的一半的时候，不仅极值对应着blob的中心位置，而且这时候的响应强度比其他尺度响应强度都强。

那么我们在检测blob时就可以使用不同的尺度计算HoG响应，选择产生最强响应的尺度，在该尺度上对应的极值就是blob的中心位置了。

对于不同尺寸的blob，理想的尺度应该是多少呢？
理论表明，对于一个圆形blob，当二维LoG算子的零点值曲线和目标圆形边缘重合时取得最强响应。

下图是LoG剖面示意

enter description here

1474428032289.jpg

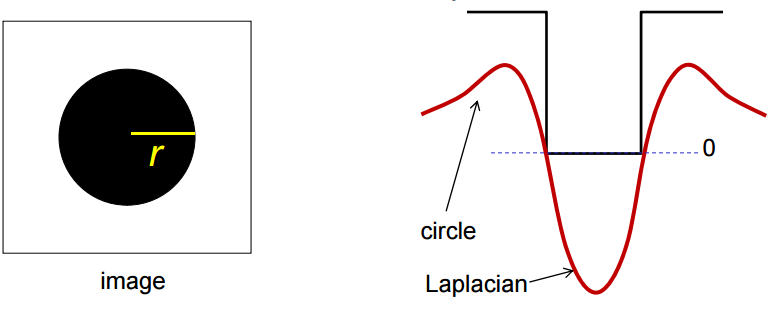
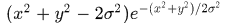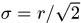所以由LoG算子的目标式1027162-20160921114134434-457373451.png可得最优尺寸为1027162-20160921114134824-1130200409.png.

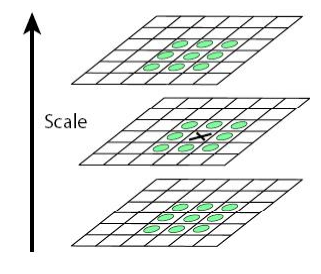
在使用LoG算子进行Blob检测时，首先在不同尺寸上对图像进行LoG，然后检测在尺度空间和图像空间都是极值的点，就是blob区域的中心点。

enter description here

1474428242180.jpg

LoG to DoG

为什么DoG可以近似LoG使用呢？
先来看看归一化之后的LoG算子(该过程将高斯函数带入化简可得)

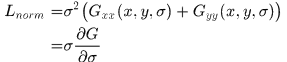
1027162-20160921114135684-936337656.png

而高斯差分算子

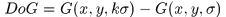
1027162-20160921114136371-335842091.png

所以

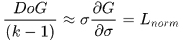
1027162-20160921114136840-539403997.png

因为k-1是常量不影响函数极值点，所以检测归一化的LoG在尺度空间的极值，即近似于检测DoG空间的极值。

DoG进行Blob检测流程
首先使用不同尺度的高斯算子对图像进行平滑
其次计算相邻尺度下平滑图像的差分图像(DoG空间)
最后在DoG空间寻找极值点

转载于:https://www.cnblogs.com/YiXiaoZhou/p/5892083.html

LOG斑点检测
AI.PLAY
11-02 4056
1.高斯拉普拉斯算子 LOG（Laplace of Guassian）算子：二维高斯函数： 拉普拉斯算子： 二维高斯函数的拉普拉斯变换：（拉普拉斯响应） 二维高斯函数的拉普拉斯变换的三维表示，和二维表示。 图像与某一函数的卷积实际就是求取图像与某一函数的相似性。当图像中的斑点尺寸与高斯拉普拉斯函数的形状趋近一致时，图像中该点的拉普拉斯响应抵达最大。通
（8-5）图像特征提取：基于LoG、DoG 和DoH 的斑点检测器
码农三叔
03-26 1293
然后，根据给定的参数（标准差、尺度因子），通过调用cv2.GaussianBlur函数创建了两个不同尺度的高斯滤波器，并对图像进行滤波操作。然后，通过遍历DoG滤波器的每个像素，检测局部极值点，并将其添加到关键点列表中。然后，通过遍历DoH滤波器的每个像素，检测局部极值点，并将其添加到关键点列表中。接下来，通过遍历滤波器的每个像素，检测局部极值点，并将其添加到关键点列表中。DoH是一种基于Hessian矩阵的特征检测方法，通过计算Hessian矩阵的行列式来检测图像中的斑点。：实现DoH斑点检测器。
斑点检测
weixin_34281537的博客
09-28 1265
1. 什么是斑点 斑点通常是指与周围有着颜色和灰度差别的区域。在实际地图中，往往存在着大量这样的斑点，如一颗树是一个斑点，一块草地是一个斑点，一栋房子也可以是一个斑点。由于斑点代表的是一个区域，相比单纯的角点，它的稳定性要好，抗噪声能力要强，所以它在图像配准上扮演了很重要的角色。 同时有时图像中的斑点也是我们关心的区域，比如在医学与生物领域，我们需要从一些X光照片或细胞显微照片中提取一些具有特...
LoG 斑点检测
Gowi的博客
04-14 1054
则可以发现随着尺度的不断增大，LoG曲线由双波谷逐渐融合成单波谷并趋于水平，导致响应也随着尺度的增大而减小，从而无法确定选定的尺度是否合适，不 知道该尺度下找到的极值点是不是对应着斑点的中心点，为了解决这一个问题，从而提出了LoG归一化的操作。斑点检测：计算不同的尺度计算LoG响应，选择产生最强响应的尺度，在该尺度上对应的极值点就是斑点的中心位置。可知当LoG的尺度与斑点的宽度匹配时，LoG的幅值在斑点的中心取得最大值（信号正负极与高斯函数相同时）用不同尺度的LoG和信号卷积，寻找幅值的最大值。
LOG斑点检测(附matlab代码)
猛码Memmat
08-03 2225
斑点检测
斑点检测(LoG,DoG) [上]
weixin_34082177的博客
09-21 738
斑点检测(LoG,DoG) [上]维基百科，LoG，DoG，DoH在计算机视觉中，斑点检测是指在数字图像中找出和周围区域特性不同的区域，这些特性包括光照或颜色等。一般图像中斑点区域的像素特性相似甚至相同，某种程度而言，斑点块中所有点是相似的。 如果将兴趣点的特性形式化表达为像素位置的函数，那么主要有两类斑点检测方法: 差分方法。这类方法主要基于函数在对应像素点处的导数。 局部极值方法。这类方...
LOG和DOG边缘检测
码灵薯的博客
08-12 4528
LOG（laplace of gaussian） laplacian 算子的定义 ▽2f(x,y)=∂f2(x,y)∂2x+∂f2(x,y)∂2y▽2f(x,y)=∂f2(x,y)∂2x+∂f2(x,y)∂2y \triangledown^2f(x,y) = \frac{\partial f^2(x,y)}{\partial^2 x} +\frac{\partial f^2(x,y)}{\p...
图像匹配中的特征点检测之斑点检测（一）
weixin_43090400的博客
11-13 5732
图像特征点检测一、斑点和角点斑点检测1、LoG算子2、SIFT算子 一、斑点和角点 全局特征容易受到噪声干扰，而局部特征比较稳定，适合用于图像匹配。 局部特征点分为斑点和角点，斑点是指与周围有着颜色和灰度差别的区域，角点则是图像中一边物体的拐角或者线条之间的交叉部分，由于斑点是一个区域，比角点的稳定性好。 斑点检测    在视觉领域，斑点检测的主要思路都是检测出图像中比它周围像...
scikit-image库----斑点检测（二十三）
Rock的博客
08-20 1881
斑点检测（Blob Detection） 在图像的明亮区域上，斑点在暗或暗上是明亮的。在此示例中，使用3种算法检测blob。在这种情况下使用的图像是Hubble eXtreme Deep Field。图像中的每个亮点都是恒星或星系。 高斯拉普拉斯（LoG） 这是最准确，最慢的方法。它计算高斯图像的拉普拉斯算子，并连续增加标准偏差并将它们堆叠在一个立方体中。 Blob是此多维数据集中的局部最大值。由...
数字图像处理与Python实现-边缘检测-高斯差分(DoG)算子边缘检测
视觉与物联智能
06-07 2869
高斯差分(DoG)算子边缘检测 高斯差分(DoG)算子边缘检测 1. 前言 2. 高斯差分(DoG)算子描述 3. 代码实现 1. 前言 在图像中，灰度或结构等信息的突变处称为边缘。边缘可以看作一个区域的结束，另一个区域的开始。利用边缘的特征，可以对图像进行分割。根据定义可以知道，利用各种算法检测到的边缘，并不代表目标的实际边缘。由于图像是二维的，而目标实物是三维的，从三维到二维的投影，已经造成了信息的丢失，再加上成像过程受光照、噪声的影响，使得有边缘的地方不一定被检测出来，而检测出来
图像的斑点检测
03-31
斑点是数字图像的主要特征，是区域检测的一种特例，是许多特征生成、目标识别等方法的重要预处理环节。斑点通常和关键点(keypoint)，兴趣点(intrestpoint)以及特征点(featurepoint)表示同一个概念。 斑点通常指与周围有着颜色和灰度区别的区域。从远处看，一棵树是一个斑点，一块草地、一栋房子也可看成斑点。主要有LoG斑点，DoH斑点以及Gilles斑点。
基于opencv的斑块检测
04-14
斑块检测斑块检测斑块检测斑块检测斑块检测斑块检测斑块检测
斑点检测资料
04-13
斑点检测资料　
缺陷检测--斑点检测
DIAJEY的博客
10-25 4889
·主要思路： 斑点检测主要使检测出图像中比它周围像素灰度值大或比周围灰度值小的区域。 一般有两种方法： 1.基于求导的微分方法，也叫微分检测器（LOG算子） 2.基于局部极值的分水岭算法（SimpleBlobDetector斑点检测算子） ·LOG斑点检测 LOG算子–高斯拉普拉斯算子（Laplace of Gaussian,LOG） ·对于二维高斯函数： exp(): ·它的拉普拉斯变换为： ·规范化后： 如上图所示，规范化后算子在二维图像上使一个圆对称函数，可以用该算子去检测图像中的斑点。
使用高斯差分DOG（Difference of Gaussians）检测图像中的斑点或者边缘
qq_51570094的博客
11-11 1122
高斯差分是指两个不同尺度下的高斯模糊图像之间的差值。具体而言，它通过对原始灰度图像应用两个具有不同标准差的高斯核进行卷积，得到两个模糊图像，然后计算这两个模糊图像之间的差分，从而生成高斯差分图像。
blob_dog(斑点检测)参数
tianyunlinger的博客
09-03 648
image：2D or 3D ndarray 输入灰度图像，斑点被假定为暗背景上的亮(白对黑)。 min_sigma：标量或标量序列，可选 高斯核函数的最小标准差。保持低电平以检测更小的斑点。高斯滤波器的标准差为每个轴作为一个序列，或作为一个单一的数字，在这种情况下，它是相等的所有轴。 Max_sigma:标量或标量序列，可选 高斯核函数的最大标准差。保持这个高度，以检测更大的斑点。高斯滤波器的标准差为每个轴作为一个序列，或作为一个单一的数字，在这种情况下，它是相等的所有轴。 sigma_ratio:浮动,
三维重建之LoG特征点检测算法流程及C++实现
冷心笑看丽美人 ~ blog
03-21 688
此乃流程 #include<iostream> #include<opencv2/opencv.hpp> #include<features2d/features2d.hpp> #include<opencv2/objdetect/objdetect.hpp> #include"opencv2/imgproc/imgproc.hpp" ...
斑点检测LOG
最新发布
04-03
### 关于斑点检测的日志文件记录方法 日志记录对于任何软件系统的运行至关重要，尤其是在涉及复杂算法的任务中，如斑点检测。以下是针对斑点检测任务设计的日志记录方法： #### 日志内容结构 为了确保日志的有效性和可追溯性，日志记录应当遵循以下标准[^1]： - **时间戳**：每条日志都需附带精确的时间标记，以便后续追踪事件发生的具体时刻。 - **日志级别**：定义清晰的日志等级（如 `DEBUG`、`INFO`、`WARNING` 和 `ERROR`），用于区分不同重要程度的信息。 - **模块/组件名称**：明确指出该日志来源于哪个具体的功能模块或子系统，例如 “SpotDetectionModule” 或者 “PreprocessingPipeline”。 - **消息内容**：提供详尽的文字描述来解释当前状态或者发生的异常情况。 - **上下文信息**：附加必要的背景资料，比如处理中的图片 ID、参数设置以及可能影响结果的关键变量。 #### 技术实现方式 在实际编码过程中可以采用 Python 的 logging 库来进行管理。下面是一个简单的例子展示如何创建适合斑点检测应用的日志框架： ```python import logging # 配置基本的日志处理器 logging.basicConfig( level=logging.DEBUG, format='%(asctime)s %(levelname)-8s [%(name)s] %(message)s', handlers=[ logging.FileHandler("spot_detection.log"), logging.StreamHandler() ] ) logger = logging.getLogger('SpotDetection') def detect_spots(image_path, threshold=0.5): try: logger.info(f'Starting spot detection on {image_path} with threshold={threshold}') # 假设这里是执行一些复杂的计算... result = {'detected': True} if not result['detected']: raise Exception("No spots detected.") logger.debug(f'Detection successful: {result}') except Exception as e: logger.error(f'Error during processing image {image_path}: {str(e)}', exc_info=True) detect_spots('/path/to/image.jpg') ``` 上述脚本设置了两种类型的输出目标——控制台和名为 `spot_detection.log` 的外部文件；通过不同的 log levels 控制哪些种类的消息会被打印出来。此外还展示了当函数正常结束时写入 debug-level message ，而遇到错误则切换到 error-level 并捕获完整的 stack trace 信息。 #### 数据存储与可视化扩展 除了基础的日志功能外，在某些情况下还需要考虑长期保存检测的结果并支持进一步的数据分析工作。这可以通过自动化的机制完成，即每次成功识别之后都将相应的元数据存放到数据库里，并定期生成汇总图表供管理层审阅[^2]。 最后值得注意的是如果项目涉及到机器学习模型，则应该额外记录训练期间的各项超参配置详情及其变化趋势作为参考依据之一[^3]。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值