1.问题描述
输入:n个数的序列<a1,a2,a3,...,an>。
输出:原序列的一个重排<a1*,a2*,a3*,...,an*>;,使得a1*<=a2*<=a3*<=...<=an*。
2. 问题分析
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
然后我们对每列进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
排序之后变为:
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94
最后以1步长进行排序(此时就是简单的插入排序了)。
对于每一列的排序,可以采用任意一个算法,本文采用变形的InsertSort( CVector<T> &vec,int start, int end, int step = 1 )。
3. 算法实现
template <typename T>
void InsertSort( CVector<T> &vec,int start, int end, int step = 1 )
{
for ( size_t i=start+step; i<vec.GetSize(); i+=step )
{
T temp = vec[i];
int j = i-step;
while ( j >= start && vec[j] > temp )
{
vec[j+step] = vec[j];
j-=step;
}
vec[j+step] = temp;
}
}
template <typename T>
void ShellSort( CVector<T> &vec )
{
const int gaps[10] = {1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905};
int i_gap = 9;
int size = vec.GetSize();
while( gaps[i_gap] >=size-1 )
i_gap--;
for( int gap = gaps[i_gap]; i_gap>=0; gap=gaps[--i_gap] )
{
//traversal each element in block
for ( int i=0; i<gap; i++ )
{
//ShellSortPart( vec, i, gap );
InsertSort<int>( vec, i, size-1, gap );
}
}
}测试:
#define DATA_MAGNITUDE 100
double random(double start, double end)
{
return start+(end-start)*rand()/(RAND_MAX + 1.0);
}
int main(int argc, char **argv)
{
CVector<int> vec1(10,2);
CVector<int> vec2(DATA_MAGNITUDE);
CVector<char> vec_txt(1000,'a');
//====================================================================
srand( unsigned(time(0)));
for ( int i=0; i<DATA_MAGNITUDE; i++ )
{
//vec2.PushBack( (int)rand()%DATA_MAGNITUDE );
vec2.PushBack( (int)random(0, DATA_MAGNITUDE) );
}
unsigned int size = 20<DATA_MAGNITUDE? 20:DATA_MAGNITUDE;
for ( size_t i =0; i < size; i++ )
{
cout<<vec2[i]<<" ";
}
cout<<endl;
//InsertSort<int>( vec2, 0, vec2.GetSize()-1 );
//BubbleSort<int>( vec2 );
//SelectSort<int>( vec2 );
ShellSort<int>( vec2 );
for ( size_t i =0; i < size; i++ )
{
cout<<vec2[i]<<" ";
}
cout<<endl;
return 0;
}
4. 算法分析
希尔排序的性能与选取的步长直接相关。
| General term (k ≥ 1) | Concrete gaps | Worst-case time complexity | Author and year of publication |
|---|---|---|---|
 | 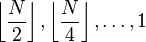 |  [when N=2p] [when N=2p] | Shell, 1959[1] |
 | 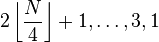 |  | Frank & Lazarus, 1960[5] |
 |  |  | Hibbard, 1963[6] |
 , prefixed with 1 , prefixed with 1 |  |  | Papernov & Stasevich, 1965[7] |
successive numbers of the form  |  |  | Pratt, 1971[8] |
 , not greater than , not greater than  |  |  | Knuth, 1973[9] |
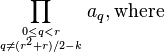
|  |  | Incerpi & Sedgewick, 1985[10] |
 , prefixed with 1 , prefixed with 1 |  |  | Sedgewick, 1986[3] |
 |  |  | Sedgewick, 1986[3] |
 |  | ? | Gonnet & Baeza-Yates, 1991[11] |
 |  | ? | Tokuda, 1992[12] |
| unknown |  | ? | Ciura, 2001[13] |
 希尔排序详解
希尔排序详解

























 580
580

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








