[解题报告] 2011 ACM-ICPC World Finals E

题目大意

题目原文：http://livearchive.onlinejudge.org/external/51/5132.pdf

在一个 RxC (1 <= R,C <= 1000) 的城市中，有 n (0 <= n <= 5*10^5) 家咖啡厅。城市中的人们都十分喜爱喝咖啡，所以城市中的某一位置的受欢迎程度往往依赖于该位置周围咖啡厅的数目。然而，不同的人为了寻找咖啡厅所愿意出行的距离是不同的，现在要求你写程序完成如下查询：

对某一个出行距离 R (0 <= R <= 10^6)，求出城市中最受欢迎的位置（能到达最多的咖啡厅，如果存在多个位置取y坐标最小，再取x坐标最小）

PS：(a,b) (c,d) 两点之间的距离为曼哈顿距离，也就是|a-c|+|b-d|

查询总数 q (1 <= q <= 20)

    Sample Input:

    4 4 5 3                -- R C n q

    1 1                      -- 接下来是 n 家咖啡馆的位置

    1 2

    3 3

    4 4

    2 4

    1                        -- 接下来是 q 次查询的 R

    2

    4

    Sample Output:

    3 (3,4)

    4 (2,2)

    5 (3,1)

Sample 中的情况对应于下图：

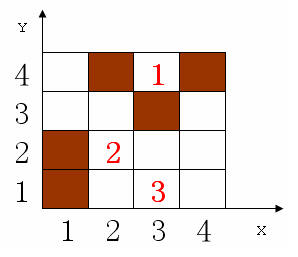
Figure 1 测试样例

暴力算法

总得来说，ACM[1]题目单个测试用例的执行时间在秒级，按现在主流 CPU 的运算速度(GHz 级)，再扣除一些常数，单个测试用例的运行时间在 O(10^8) 以内都是可以接受的。而本题每个测试用例有至多 20 次查询，所以完成每次查询的时间复杂度应该控制在 O(10^7) 以内。

首先，读完题后，我们很容易想到最暴力的算法：对于每一次查询，我们逐一检查城市中的所有位置，统计距其 R 范围内所有咖啡店的数目，然后选择最优位置输出即可，因为距一个位置 R 范围的位置数目为 O(R^2)，这样每一次查询的时间复杂度为 O(10^6*R^2)。因为 R 很大，所以 O(10^6*R^2) >> O(10^7)。

暴力算法无法满足题目的时间需求，这时有可能是我们最初的算法错误，需要从根本上切换思考问题的方向，但也有可能是在原始算法上仍然存在改进的可能。本题就是后者，通过观察我们看到，如果我们有能力将"统计距一个位置 R 范围内的咖啡店数目"这步操作从 O(R^2) 的复杂度降到 O(10)，则问题得到解决。

从O(R^2) 降到 O(R)

那么如何降低这步操作的复杂度呢？从直观上，我们容易想到，距一个位置 R 范围的所有位置构成一个菱形区域，两个相邻位置的菱形区域具有大量重合，如下图所示。

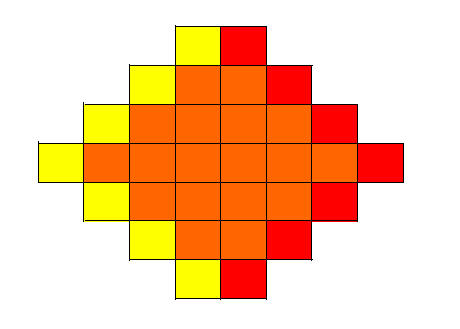
Figure 2 相邻位置的重叠统计（R=3）

如果对每一个位置进行 O(R^2) 次统计，则其中包含了大量的冗余统计（橙色部分）。去除重复统计，在已知黄色区域内咖啡馆数目NY的情况下，红色区域内咖啡馆的数目：

NR = NY – 黄色位置包含的咖啡馆数目 + 红色位置包含的咖啡馆数目

这样，即使一个个统计这些黄/红色位置，也将复杂度从O(R^2) 降到了 O(R)，但是因为 R 很大，这还不够。

从O(R) 降到 O(logR)

这一步需要一些 Hard Knowledge[2]，如果你有类似线段树、树状数组等数据结构方面的知识的话，很容易想到；如果没有的话，恐怕很困难。

在这个坐标系统中，分别构造斜率为 +1和 -1的两组树状数组（或类似数据结构），则可以在O(logR) 的时间内计算出黄/红色位置包含的咖啡馆数目。

附上我的代码，你可以去这里提交代码，验证你算法的正确性。

View Code

#include < cstdio >
#include < cstring >
#include < algorithm >

// #define debug(fmt, ...) printf(fmt, ## __VA_ARGS__)
#define debug(fmt, ...)

const int N = 1024 ;

// TA: tree array
short posTA[N * 2 ][N], negTA[N * 2 ][N];
int dx, dy, n, q;
int sum[N][N];

// pos tree array index
inline int posi( int x, int y) {
return y - x + N;
}
inline int negi( int x, int y) {
return y + x;
}

inline int lowbit( int x) { return x &- x;}
void updateTA( short TA[], int pos) {
while (pos <= dx) {
TA[pos] ++ ;
pos += lowbit(pos);
}
}

int update( int x, int y) {
updateTA(posTA[posi(x, y)], x);
updateTA(negTA[negi(x, y)], x);
}

int queryTA( short TA[], int pos) {
int res = 0 ;
while (pos > 0 ) {
res += TA[pos];
pos -= lowbit(pos);
}
return res;
}
// x1 < x2
int query( short TA[], int x1, int x2) {
x1 = std::max( 1 , x1); x2 = std::min(x2, dx);
return queryTA(TA, x2) - queryTA(TA, x1 - 1 );
}

enum { UP, RIGHT, DOWN, LEFT, };
int vx[] = { 0 , 1 , 0 , - 1 };
int vy[] = { 1 , 0 , - 1 , 0 };

void init( int x[], int y[], int sx, int sy, int nStep) {
int i;
for (i = 0 ; i < 4 ; ++ i) {
x[i] = sx + nStep * vx[i];
y[i] = sy + nStep * vy[i];
}
}

// (x,y) 点所在的45度线是否与矩形有交集
inline bool isPos( int x, int y) {
return 1 - dx <= y - x && y - x <= dy - 1 ;
}
inline bool isNeg( int x, int y) {
return 2 <= x + y && x + y <= dx + dy;
}

int getSum( int y, int x, int m) {
int i, res = 0 ;
int vtx[ 4 ], vty[ 4 ];
if (x == 1 ) {
if (y == 1 ) {
for (i = 0 ; i <= m; ++ i) {
res += query(negTA[negi(x, y)], 1 , x + i);
y += vy[UP];
}
} else {
init(vtx, vty, x, y, m);
res += sum[x][y - 1 ];
if (isNeg(vtx[DOWN] + vx[DOWN], vty[DOWN] + vy[DOWN]))
res -= query(negTA[negi(vtx[DOWN] + vx[DOWN], vty[DOWN] + vy[DOWN])], vtx[LEFT], vtx[DOWN]);
if (isNeg(vtx[UP], vty[UP]))
res += query(negTA[negi(vtx[UP], vty[UP])], vtx[UP], vtx[RIGHT]);
if (isPos(vtx[DOWN] + vx[DOWN], vty[DOWN] + vy[DOWN]))
res -= query(posTA[posi(vtx[DOWN] + vx[DOWN], vty[DOWN] + vy[DOWN])], vtx[DOWN] + 1 , vtx[RIGHT]);
if (isNeg(vtx[UP], vty[UP]))
res += query(posTA[posi(vtx[UP], vty[UP])], vtx[LEFT], vtx[UP] - 1 );
}
} else {
init(vtx, vty, x, y, m);
res += sum[x - 1 ][y];
if (isNeg(vtx[LEFT] + vx[LEFT], vty[LEFT] + vy[LEFT]))
res -= query(negTA[negi(vtx[LEFT] + vx[LEFT], vty[LEFT] + vy[LEFT])], vtx[LEFT] - 1 , vtx[DOWN] - 1 );
if (isNeg(vtx[RIGHT], vty[RIGHT]))
res += query(negTA[negi(vtx[RIGHT], vty[RIGHT])], vtx[UP], vtx[RIGHT]);
if (isPos(vtx[LEFT] + vx[LEFT], vty[LEFT] + vy[LEFT]))
res -= query(posTA[posi(vtx[LEFT] + vx[LEFT], vty[LEFT] + vy[LEFT])], vtx[LEFT], vtx[UP] - 1 );
if (isNeg(vtx[RIGHT], vty[RIGHT]))
res += query(posTA[posi(vtx[RIGHT], vty[RIGHT])], vtx[DOWN], vtx[RIGHT] - 1 );
}
return res;
}

int main(){
int caseNum = 0 ;
int x, y, m;
int i, j;
int best, bestx, besty, val;
while ( true ) {
scanf( " %d %d %d %d " , & dx, & dy, & n, & q);
if (dx == 0 ) break ;
memset(posTA, 0 , sizeof (posTA));
memset(negTA, 0 , sizeof (negTA));
while (n -- ) {
scanf( " %d %d " , & x, & y);
update(x, y);
}

printf( " Case %d:\n " , ++ caseNum);
while (q -- ) {
best = - 1 ;
scanf( " %d " , & m);
for (j = 1 ; j <= dy; ++ j) {
for (i = 1 ; i <= dx; ++ i) {
val = sum[i][j] = getSum(j, i, m);
if (val > best) {
best = val, bestx = i, besty = j;
}
debug( " %d " , sum[i][j]);
}
debug( " \n " );
}
printf( " %d (%d,%d)\n " , best, bestx, besty);
}
}
return 0 ;
}

最后，恭喜ZJU Final夺冠[4]。如果你还想继续了解其他题目的解法，[3]是一份大牛写的部分解题报告，我只会做 E 这种简单题（参考[4]最下面的题目统计），绝大部分题目很无力。

Reference：

[1] ACM-ICPC http://cm.baylor.edu/welcome.icpc

[2] Hard Knowledge http://mindhacks.cn/2008/04/18/learning-from-polya/

[3] WF2011部分题目解题报告 http://blog.renren.com/share/221472268/6796549013/

[4] WF2011最终排名与题目数据统计 http://scrool.se/icpc/wf2011/

转载于:https://www.cnblogs.com/beardman/archive/2011/06/01/ACM-ICPC-WF2011-E-solution.html