插入排序讲解

最新推荐文章于 2025-08-17 11:00:00 发布

weixin_34124651

最新推荐文章于 2025-08-17 11:00:00 发布

阅读量75

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/YUJIE666/p/9866193.html

本文详细介绍了一种简单直观的排序算法——插入排序。通过一个具体的Java实现案例，展示了如何使用插入排序对整数数组进行排序。文章解释了算法的工作原理，包括最坏情况的时间复杂度为Θ(n²)，并对比了其与归并排序在不同数据规模下的性能表现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Θ2018-10-28 16:53:20 开始写

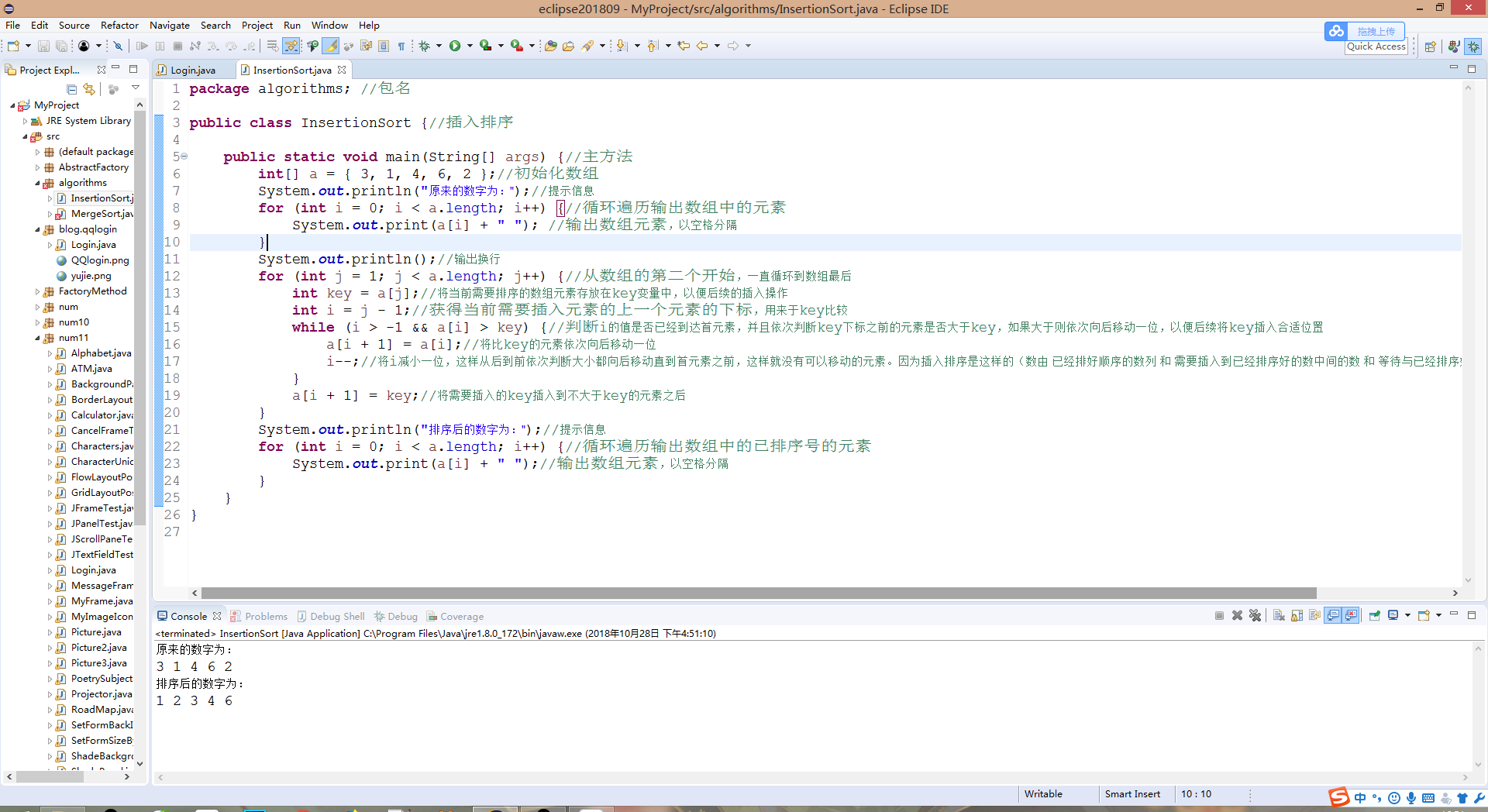
 1 package algorithms; //包名
 2 
 3 public class InsertionSort {//插入排序
 4 
 5     public static void main(String[] args) {//主方法
 6         int[] a = { 3, 1, 4, 6, 2 };//初始化数组
 7         System.out.println("原来的数字为：");//提示信息
 8         for (int i = 0; i < a.length; i++) {//循环遍历输出数组中的元素
 9             System.out.print(a[i] + " "); //输出数组元素，以空格分隔
10         }
11         System.out.println();//输出换行
12         for (int j = 1; j < a.length; j++) {//从数组的第二个开始，一直循环到数组最后
13             int key = a[j];//将当前需要排序的数组元素存放在key变量中，以便后续的插入操作
14             int i = j - 1;//获得当前需要插入元素的上一个元素的下标，用来于key比较
15             while (i > -1 && a[i] > key) {//判断i的值是否已经到达首元素，并且依次判断key下标之前的元素是否大于key，如果大于则依次向后移动一位，以便后续将key插入合适位置
16                 a[i + 1] = a[i];//将比key的元素依次向后移动一位
17                 i--;//将i减小一位，这样从后到前依次判断大小都向后移动直到首元素之前，这样就没有可以移动的元素。因为插入排序是这样的（数由 已经排好顺序的数列 和 需要插入到已经排序好的数中间的数 和 等待与已经排序好的数进行插入操作的序列）
18             }
19             a[i + 1] = key;//将需要插入的key插入到不大于key的元素之后
20         }
21         System.out.println("排序后的数字为：");//提示信息
22         for (int i = 0; i < a.length; i++) {//循环遍历输出数组中的已排序号的元素
23             System.out.print(a[i] + " ");//输出数组元素，以空格分隔
24         }
25     }
26 }

说明：

首先注解很详细。

最坏情况：Θ（n²）

在数量较少时插入排序速度比归并排序快，但超过某个临界值时归并排序远远超过插入排序

关于插入排序以后还会补充

谢谢、Thank you、Salamat Do（撒拉玛特朵）、あリがCám o*n（嘉蒙）とゥ（阿里嘎都）、감사합니다 （勘三哈咪瘩）、terima Kasih（得力马卡系）、kob-khun（寇布库恩）、dhanyavaad（达尼阿瓦德）、toda（透达）、te?ekkür ederim（特谢库尔埃戴里姆）、Dzie,kuje（以库以而）、Spasibo（思巴喜柏）、Danke（但可）、shokran（休克朗）、Obrigada（欧布哩嘎搭）、dank u（当Q）、Merci（梅呵西）、Gracias（格拉喜亚思）、Grazie（格啦姬）、Благодарности、Tak、Kiitos、Díky、Hvala、Mul?umesc、Takk、Ευχαριστ

转载于:https://www.cnblogs.com/YUJIE666/p/9866193.html