2.4 条件概率
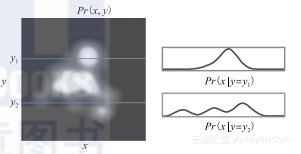
图2-5 条件概率x和y的联合概率密度函数以及两个条件概率分布Pr(xy=y1)和Pr(xy=y2)。通过从联合概率密度函数中提取切片并规范化,确保区域一致。同样的操作也适用于离散分布给定y取y时x的条件概率,是随机变量x在y取固定值y时x的相对概率的取值。这个条件概率记为Pr(xy=y*)。“”可以理解为“给定”。
条件概率Pr(xy=y)可以由联合分布Pr(x,y)计算出来。特别是,计算联合分布中某个恰当的切片Pr(x,y=y)(见图2-5)。切片值表示出当y=y*时x取不同值的相对概率,但其本身没有形成有效的概率分布。因为它们仅构成联合分布的一小部分,其总和不会是1,而联合概率自身总和为1。为计算条件概率分布,因此需要规范化切片中的总概率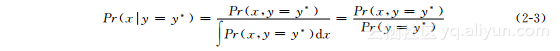
其中,使用边缘概率关系式(式(2-1))去简化分母。通常情况下不会显式定义y=y*,所以条件概率关系式可简化缩写为: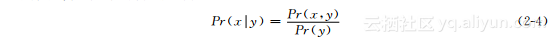
重新整理得到: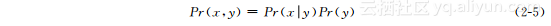
由对称性也可得: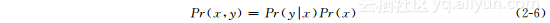
当有两个以上的变量时,可以不断用条件概率分布将联合概率分布分解为乘积形式: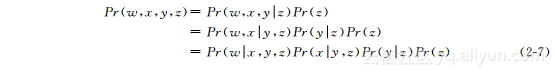







 本文详细解释了条件概率的概念,包括如何从联合概率密度函数中提取特定切片并进行规范化以获得条件概率分布。此外还介绍了条件概率与联合概率之间的数学关系,并展示了如何利用条件概率将多个变量的概率分布进行分解。
本文详细解释了条件概率的概念,包括如何从联合概率密度函数中提取特定切片并进行规范化以获得条件概率分布。此外还介绍了条件概率与联合概率之间的数学关系,并展示了如何利用条件概率将多个变量的概率分布进行分解。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








