70. Climbing Stairs

爬楼梯问题的两种算法实现

最新推荐文章于 2024-01-18 13:59:59 发布

weixin_34116110

最新推荐文章于 2024-01-18 13:59:59 发布

阅读量50

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/ucas/p/5809624.html

本文探讨了经典的爬楼梯问题，并提供了两种不同的算法实现方案：一种是使用迭代的动态规划方法；另一种则是利用数学公式直接求解。两种方法各有优劣，前者易于理解且计算效率高，后者虽然复杂度较高但代码简洁。

问题描述

解决方案

我的解决方法

class Solution {
public:
    int climbStairs(int n) {
        int a=1,b=1;
        for(int i=1;i<n;++i)
        {
            b+=a;
            a=b-a;
        }
        return b;
    }
};

网上的解决方法

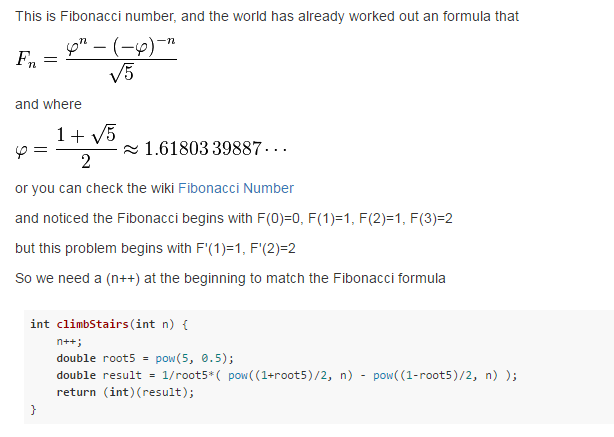
class Solution {
public:
    int climbStairs(int n) {
        return (pow((1.0+sqrt(5.0))/2.0,n+1)-pow((1.0-sqrt(5.0))/2.0,n+1))/sqrt(5.0);
    }
};

转载于:https://www.cnblogs.com/ucas/p/5809624.html

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。