Dijkstra 算法

算法的核心思想：在尚未使用的顶点中，d[i]最小的顶点就是最短距离已经确定的顶点

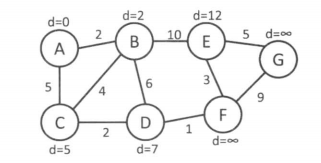
解释：以图1-1为例，假设A，B，C已经被标记，则剩下的点可以认为经过A，B，C三点的松弛操作(看通过这个点作为中转站会不会使得其他点离起点更近)。

那么在被标记的顶点中，找出d[i]最小的顶点，就可以认为它就是最短距离已经确定的顶点。我们用反证法，假如它的值不是最短距离，那么你想A，B，C三点已经都对其余剩下所有的点进行了松弛操作，那么现在就不能再使其他点到起点的距离变得更短；那么就只能想办法通过其他点让它到起点的距离变短，然而由于不存在负边，不可能通过其他的点让它到起点的距离变得更短(不会在之后的更新中变小)。因此，就可以认为它就是最短距离已经确定的顶点。

自然而然我们就发现Dijkstra 算法不适合处理有负边的情况

 

 模板如下：

int cost[MAX_N][MAX_N]; //cost[u][v]表示边e(u,v)的权值(不存在时设为INF) 
int d[MAX_N]; //图上各点到顶点s的最短距离 
int vis[MAX_N]; //已经使用过的图
int n; //顶点数 

memset(vis, 0, sizeof(vis));
memset(d, 0x3f, sizeof(d));
d[s] = 0;
    
while (1) {
    int v = -1;
    //从尚未使用过的顶点中选择一个距离最小的顶点 
    for (int i = 1; i <= n; i++)
        if (vis[i]==0 && (v==-1||d[i]<d[v])) v = i;
        
    if (v==-1) break;
    vis[v] = 1;
        
    for (int i = 1; i <= n; i++)
        d[i] = min(d[i], d[v]+cost[v][i]);//对周围的点进行松弛操作 
}

---

仔细想想，其实我们还能进一步优化这个算法，需要优化的是数值的插入(更新)和取出最小值两个操作，因此使用堆就可以了。

优化后的模板入下：

struct edge {int to, cost};
typedef pair<int , int> P;

int V;
vector<edge> G[MAX_V];
int d[MAX_V];

priority_queue<P, vector<P>, greater<P> >que;
fill(d, d+V, INF);
d[s] = 0;
que.push(P(0, s));

while (!que.empty()) {
    P p = que.top(); que.pop();
    int v = p.second;
    if (d[v]<p.first) continue;
    for (int i = 0; i < G[v].size(); i++) {
        edge e = G[v][i];
        if(d[e.to]>d[v]+e.cost) {
            d[e.to] = d[v]+e.cost;
            que.push(P(d[e.to, e.to]));
        }
    }
}
 

 

转载于:https://www.cnblogs.com/wizarderror/p/10902223.html