【leetcode】Preimage Size of Factorial Zeroes Function

题目如下：

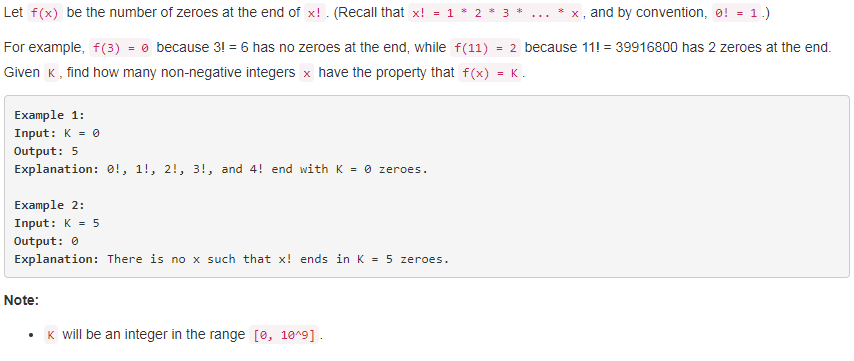
解题思路：《编程之美》中有一个章节是不要被阶乘吓倒，里面讲述了“问题一：给定一个整数N，那么N的阶乘末尾有多少个0呢？例如N = 10， N! = 362800，N! 的末尾有两个0.” 这个问题的解法。本题就是在这个问题的基础上把输入和输出倒过来了。首先，对于输入参数K，我们可以知道输出结果的范围是[0,K*5]，同时我们也可以知道，对于任意两个正整数i,j (i>j)，i的阶乘一定是大于j的阶乘的，那么i的阶乘末尾0的数量也一定是大于或者j的阶乘末尾0的数量，既然是一个单调递增的关系，那么就可以采用二分查找来判断输入参数K存不存在。最后，题目要求的返回值是满足阶乘值末尾0的数量等于K的数字的个数，这也很简单，因为我们从《编程之美》的案例中可以知道，阶乘值每多一个5，0的数量就会变化。因此，如果K存在，那么满足条件的数字就是5，如果不存在则是0。

代码如下：

class Solution(object):
    def calcFactorial(self,v):
        n = v
        count = 0
        while n > 0:
            count += n / 5
            n = n / 5
        return count
    def preimageSizeFZF(self, K):
        high = K*5
        low = 0
        while low <= high:
            mid = (high + low)/2
            if self.calcFactorial(mid) < K:
                low = mid +1
            elif self.calcFactorial(mid) > K:
                high = mid - 1
            else:
                return 5
        return 0
        

 

转载于:https://www.cnblogs.com/seyjs/p/8583803.html