魔方阵

魔方阵，又叫幻方，在我国古代称为“纵横图”。由N^2个自然数构成的幻方叫N阶幻方，每行、每列及两对角线上各数之和都相等。魔方阵的求解要分三种情况讨论，N为奇数、N是偶数且是4的倍数，N是偶数但不是4的倍数。

一、N为奇数的情况

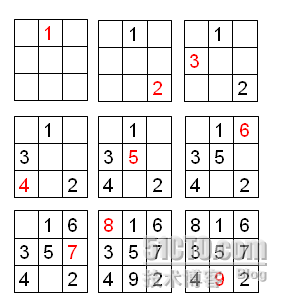
1、把1放在N*N方阵中的第一行中间一列。

2、后一个数存放的行数比前一个数存放的行数减1，若这个行数为0，则取行数为N；  
3、后一个数存放的列数比前一个数存放的列数加1，若这个列数为N+1，则取列数为1；  
4、如果前一个数是N的倍数，则后一个数存放的列数不变，而行数加1。 即放在前一个数的下面，也可以按照2、3算得的现在这个数位置上已经有数时直接把现在这个数放在它上一个数字的下面。

下图是N=3时候的步骤，依次从左到右，从上到下

二、N为偶数且N为4的倍数的时候

先将1至N*N由小到大的顺序，从第一行开始依左上到右下的顺序填入N*N的方阵中，然后将N*N的方阵以4 行4列划分为若干个4*4的小方阵，再将所有4*4小方阵的两个对角线上的数字划掉，之后将所有被划掉的数字重新由大到小的进行排列（注意是所有的一起排列，不是每个4*4小阵内部排列），然后再将这些数字按排列顺序由N*N方阵 的第一行开始，放入被划掉的格子中去。

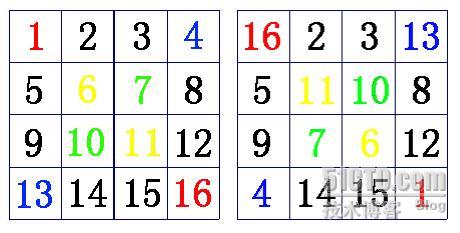
N=4的情况如下图，带颜色的是需要交换的数字，且相同的数字之间进行交换。

也可以不用排序，但仍然是对角线上的数字需要变化，对于数字x，将其变为数字N*N+1-x。

例如上图中x=1时，将x变为4*4+1-1=16。

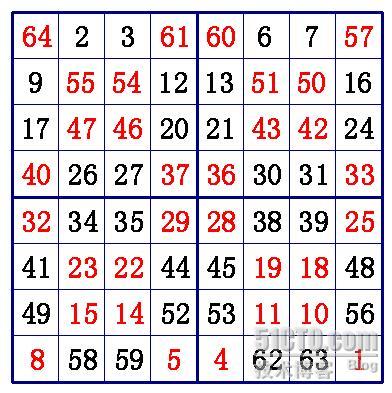
N=8的情况如下图

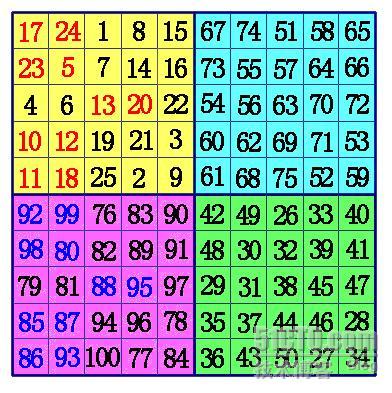
三、N为偶数但不是4的倍数的情况 设N=4k+2

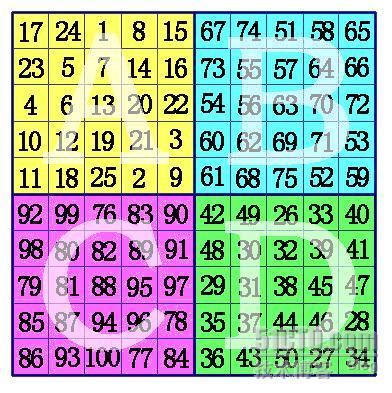
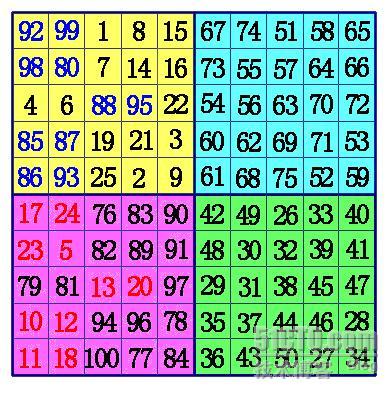
1、把方阵分为A，B，C，D四个象限，这样每一个象限肯定是奇数阶。依次在A象限，D象限，B象限，C象限按奇数阶幻方的填法填数。（注意不是ABCD的顺序）

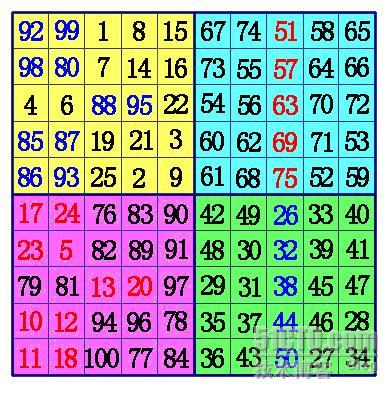
2、在A象限的中间行、中间格开始，按自左向右的方向，标出k格。A象限的其它行则标出最左边的k格。将这些格，和C象限相对位置上的数，互换位置。

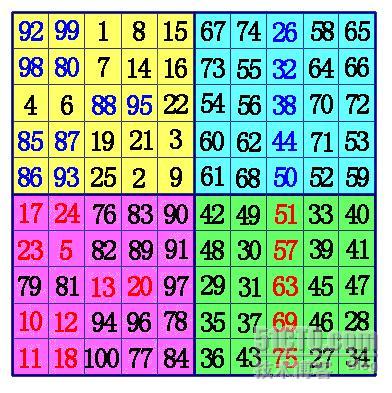
3、在B象限任一行的中间格，自右向左，标出k-1列。(注：6阶幻方由于k-1=0，所以不用再作B、D象限的数据交换)， 将B象限标出的这些数，和D象限相对位置上的数进行交换，就形成幻方。

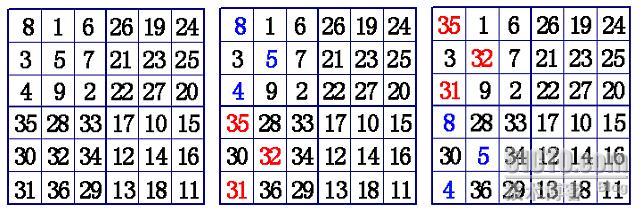
下面是6阶幻方的填法：6＝4×1＋2，这时k＝1

 

以上偶数的情况摘自 http://hi.baidu.com/chisir001/blog/item/47ac9da843b7b5f61f17a2ec.html

下面是我用C++编写的代码，只注重了方法，没重效率

#include <iostream>
using namespace std;
void check( int **arr, int n)
{
   int r;
         int c;
         int sum[4]={0};
    
         for (r=0;r<n;r++)
        {
                sum[0]=0;
                sum[1]=0;
    
                sum[2]+=arr[r][r];
                sum[3]+=arr[n-r-1][r];
    
                 for (c=0;c<n;c++)
                {
                        sum[0]+=arr[r][c];
                        sum[1]+=arr[c][r];
                }
    cout<< "第"<<r+1<< "行："<<sum[0]<< "\t第"<<r+1<< "列："<<sum[1]<<endl;
        }
  cout<< "右 斜："<<sum[2]<< "\t左 斜："<<sum[3]<<endl;;
    
}
void odd( int **cub, int n)
{
  cub[0][(n-1)/2]=1;
   int prex=0; int prey=(n-1)/2;
   for( int k=2;k<=n*n;k++)
  {   int nowx,nowy;
   if((k-1)%n==0)
  {
    nowx=prex+1;
    nowy=prey;
  }
        
   else
  {
    nowx=prex-1;
    nowy=prey+1;
     if(nowx<0)
      nowx=n-1;
     if(nowy>=n)
      nowy=0;
    
  }
  cub[nowx][nowy]=k;
  prex=nowx;
  prey=nowy;
    
    
    
    
  }
    
}
void main()
{     int n;
cout<< "请输入大于2的正整数n\n";
cin>>n;
int **cub= new int*[n];
for( int i=0;i<n;i++)
{
  cub[i]= new int[n];
  memset(cub[i],0, sizeof( int)*n);
}
if(n%2) //奇数
{
  odd(cub,n);
    
    
}
else if(n%4==0) //能被4整除的情况
{
   int temp[8]={0};
   int cnt=1;
   for( int i=0;i<n;i++)
     for( int j=0;j<n;j++)
    {
      cub[i][j]=cnt;
      cnt++;
    }
    
     for( int p=0;p<=4*(n/4-1);p=p+4)
       for( int q=0;q<=4*(n/4-1);q=q+4)
      {    
         for( int m=0;m<4;m++)
        {
          cub[m+p][m+q]=n*n+1-cub[m+p][m+q];
          cub[m+p][3-m+q]=n*n+1-cub[m+p][3-m+q];
        }
        
      }
        
}
else     //不能被4整除的偶数
{
   int nn=n/2;
   int k=n/4;
   int **smallcub= new int *[nn];
   for( int i=0;i<nn;i++)
  {
    smallcub[i]= new int[nn];
    memset(smallcub[i],0, sizeof( int)*nn);
  }
  odd(smallcub,nn);
   for(i=0;i<nn;i++)
     for( int j=0;j<nn;j++)
    {
      cub[i][j]=smallcub[i][j];
      cub[i+nn][j+nn]=smallcub[i][j]+nn*nn;
      cub[i][j+nn]=smallcub[i][j]+2*nn*nn;
      cub[i+nn][j]=smallcub[i][j]+3*nn*nn;
    }
    
     int middle=(nn-1)/2;
     for( i=0;i<nn;i++)
       for( int j=0;j<k;j++)
      {
         if(i==middle)
        {
           int temp=cub[i][middle+j];
          cub[i][middle+j]=cub[i+nn][middle+j];
          cub[i+nn][middle+j]=temp;
        }
         else
        {
           int temp=cub[i][j];
          cub[i][j]=cub[i+nn][j];
          cub[i+nn][j]=temp;
            
        }
        
      }
        
       for(i=0;i<nn;i++)
      {
         for( int j=0;j<k-1;j++)
        {
            
           int temp=cub[i][middle-j+nn];
          cub[i][middle-j+nn]=cub[i+nn][middle-j+nn];
          cub[i+nn][middle-j+nn]=temp;
            
        }
      }
        
        
        
}
for(i=0;i<n;i++)
{   for( int j=0;j<n;j++)
{
  cout<<cub[i][j]<< "\t ";
    
}
cout<<endl;
}
check(cub,n);

}

 

转载于:https://blog.51cto.com/buptdtt/706173