2.3 仿真
本节介绍用积分法对下述状态方程描述的非线性系统进行计算机仿真:
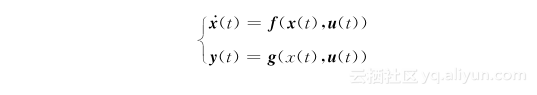
该方法是一种近似法,但容易理解,并且对于描述大多数机器人系统的行为是足够的。
2.3.1 欧拉法


2.3.2 龙格库塔法


2.3.3 泰勒法
欧拉法(实际上是1阶泰勒法)可以扩展到更高的阶数。在不失普遍性的前提下,让我们来看看如何扩展到二阶。我们有:
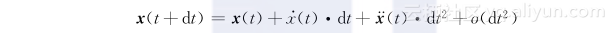
但:

因此,积分方法变为:
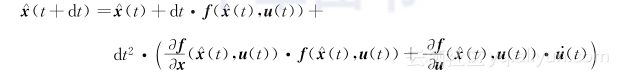
本节介绍用积分法对下述状态方程描述的非线性系统进行计算机仿真:
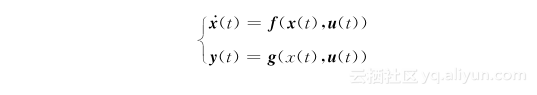
该方法是一种近似法,但容易理解,并且对于描述大多数机器人系统的行为是足够的。




欧拉法(实际上是1阶泰勒法)可以扩展到更高的阶数。在不失普遍性的前提下,让我们来看看如何扩展到二阶。我们有:
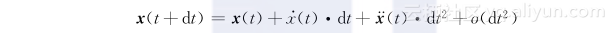
但:

因此,积分方法变为:
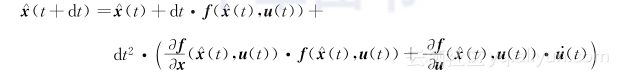

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


